题目内容
如图,正四棱锥中P-ABCD,点E,F分别在棱PA,BC上,且AE=2PE,(1)问点F在何处时,EF⊥AD?
(2)当EF⊥AD且正三角形PAB的边长为a时,求点F到平面PAB的距离;
(3)在第(2)条件下,求二面角C-PA-B的大小.

【答案】分析:本题利用空间直角坐标系,求出相关向量,利用数量积和距离公式解答.
(1)先作PO⊥平面ABCD,依题意O是正方形ABCD的中心,如图建立空间坐标系.
设AB=a,PO=b,写出点的坐标: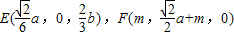 ,利用向量的数量积即可证得EF⊥AD;
,利用向量的数量积即可证得EF⊥AD;
(2)设点F到平面PAB的距离为d.先求得面PAB的法向量,再结合向量的数量积即可求出点F到平面PAB的距离;
(3)设二面角C-AP-B的平面角为θ,先求出平面PAB的法向量为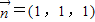 和平面PAC的法向量,最后利用夹角公式即可求得二面角C-PA-B的大小.
和平面PAC的法向量,最后利用夹角公式即可求得二面角C-PA-B的大小.
解答:解:(1)作PO⊥平面ABCD,依题意O是正方形ABCD的中心,如图建立空间坐标系.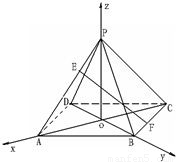
设AB=a,PO=b, .(2分)
.(2分)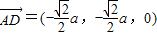 ,
,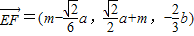 .
.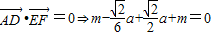
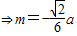 .
.
∴当F为BC的三等分点(靠近B)时,有EF⊥AD..(4分)
(2)设点F到平面PAB的距离为d.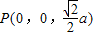 ,
,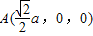 ,
,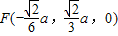
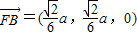
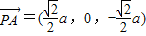 ,
,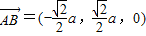 ,设面PAB的法向量为
,设面PAB的法向量为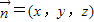
∴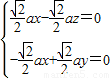
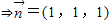 ,(6分)
,(6分)
∴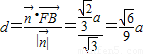 .(8分)
.(8分)
(3)设二面角C-AP-B的平面角为θ,平面PAB的法向量为 .
.
设平面PAC的法向量为 ,∴
,∴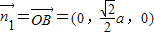 .(10分)
.(10分)
∴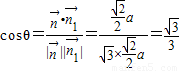 .∴
.∴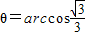 .(12分)
.(12分)
点评:本题考查直线与平面垂直,二面角,点的平面的距离,考查空间想象能力,逻辑思维能力,是中档题.
(1)先作PO⊥平面ABCD,依题意O是正方形ABCD的中心,如图建立空间坐标系.
设AB=a,PO=b,写出点的坐标:
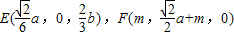 ,利用向量的数量积即可证得EF⊥AD;
,利用向量的数量积即可证得EF⊥AD;(2)设点F到平面PAB的距离为d.先求得面PAB的法向量,再结合向量的数量积即可求出点F到平面PAB的距离;
(3)设二面角C-AP-B的平面角为θ,先求出平面PAB的法向量为
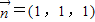 和平面PAC的法向量,最后利用夹角公式即可求得二面角C-PA-B的大小.
和平面PAC的法向量,最后利用夹角公式即可求得二面角C-PA-B的大小.解答:解:(1)作PO⊥平面ABCD,依题意O是正方形ABCD的中心,如图建立空间坐标系.

设AB=a,PO=b,
 .(2分)
.(2分)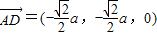 ,
,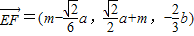 .
.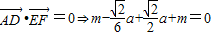
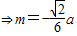 .
.∴当F为BC的三等分点(靠近B)时,有EF⊥AD..(4分)
(2)设点F到平面PAB的距离为d.
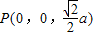 ,
,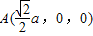 ,
,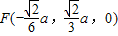
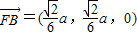
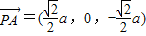 ,
,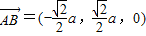 ,设面PAB的法向量为
,设面PAB的法向量为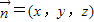
∴
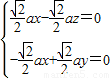
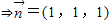 ,(6分)
,(6分)∴
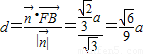 .(8分)
.(8分)(3)设二面角C-AP-B的平面角为θ,平面PAB的法向量为
 .
.设平面PAC的法向量为
 ,∴
,∴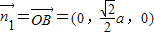 .(10分)
.(10分)∴
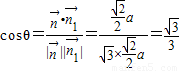 .∴
.∴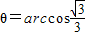 .(12分)
.(12分)点评:本题考查直线与平面垂直,二面角,点的平面的距离,考查空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
相关题目
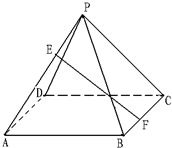 如图,正四棱锥中P-ABCD,点E,F分别在棱PA,BC上,且AE=2PE,
如图,正四棱锥中P-ABCD,点E,F分别在棱PA,BC上,且AE=2PE, 12、如图在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC,则动点P的轨迹与△SCD组成的相关图形是( )
12、如图在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC,则动点P的轨迹与△SCD组成的相关图形是( ) 如图,正四棱锥P-ABCD中,PA=AB,点M,N分别在PA,BD上,且
如图,正四棱锥P-ABCD中,PA=AB,点M,N分别在PA,BD上,且 如图,正四棱锥P-ABCD中,PA=2,AB=1,M是侧棱PC的中点,O为底面正方形的中心.
如图,正四棱锥P-ABCD中,PA=2,AB=1,M是侧棱PC的中点,O为底面正方形的中心.