题目内容
设F1,F2是椭圆 两个焦点,P是椭圆上一点,且|PF1|-|PF2|=1,若∠F1PF2=α,则cos2α=________.
两个焦点,P是椭圆上一点,且|PF1|-|PF2|=1,若∠F1PF2=α,则cos2α=________.
-
分析:根据椭圆的定义、标准方程,以及简单性质求出|PF1|= ,|PF2|=
,|PF2|= ,△F1PF2中,由余弦定理求得 cosα 的值,再由二倍角公式求出cos2α的值.
,△F1PF2中,由余弦定理求得 cosα 的值,再由二倍角公式求出cos2α的值.
解答:由题意可得a=2,b= ,c=1,F1(-1,0),F2(1,0),|PF1|-|PF2|=1,|PF1|+|PF2|=4,
,c=1,F1(-1,0),F2(1,0),|PF1|-|PF2|=1,|PF1|+|PF2|=4,
∴|PF1|= ,|PF2|=
,|PF2|= .
.
△F1PF2中,由余弦定理可得|F1F2|2=|PF1|2+|PF2|2-2|PF1|•|PF2|cosα,
即4= +
+ -2×
-2× ×
× cosα,
cosα,
∴cosα= ,
,
∴cos2α=2cos2α-1=- .
.
故答案为:- .
.
点评:本题主要考查椭圆的定义、标准方程,以及简单性质,二倍角公式和余弦定理的应用,求出|PF1|= ,|PF2|=
,|PF2|= ,是解题的突破口.
,是解题的突破口.

分析:根据椭圆的定义、标准方程,以及简单性质求出|PF1|=
 ,|PF2|=
,|PF2|= ,△F1PF2中,由余弦定理求得 cosα 的值,再由二倍角公式求出cos2α的值.
,△F1PF2中,由余弦定理求得 cosα 的值,再由二倍角公式求出cos2α的值.解答:由题意可得a=2,b=
 ,c=1,F1(-1,0),F2(1,0),|PF1|-|PF2|=1,|PF1|+|PF2|=4,
,c=1,F1(-1,0),F2(1,0),|PF1|-|PF2|=1,|PF1|+|PF2|=4,∴|PF1|=
 ,|PF2|=
,|PF2|= .
.△F1PF2中,由余弦定理可得|F1F2|2=|PF1|2+|PF2|2-2|PF1|•|PF2|cosα,
即4=
 +
+ -2×
-2× ×
× cosα,
cosα,∴cosα=
 ,
,∴cos2α=2cos2α-1=-
 .
.故答案为:-
 .
.点评:本题主要考查椭圆的定义、标准方程,以及简单性质,二倍角公式和余弦定理的应用,求出|PF1|=
 ,|PF2|=
,|PF2|= ,是解题的突破口.
,是解题的突破口. 
练习册系列答案
相关题目
设F1,F2是椭圆
+
=1(a>b>0)的两个焦点,P是椭圆上一点,∠F1PF2,=90°则该椭圆离心率的最小值为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
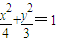 两个焦点,P是椭圆上一点,且|PF1|-|PF2|=1,若∠F1PF2=α,则cos2α= .
两个焦点,P是椭圆上一点,且|PF1|-|PF2|=1,若∠F1PF2=α,则cos2α= .