题目内容
已知关于x的实系数一元二次方程在复数集中两个根α、β,有下列结论:①α、β互为共轭复数;②α+β=-
,α•β=
;③b2-4ac≥0;④|α-β|=
.正确结论的个数是( )
| b |
| a |
| c |
| a |
| (α+β)2-4αβ |
| A、1 | B、2 | C、3 | D、4 |
分析:若两个根α、β 都为实根,则①不成立,若两个根α、β 都为虚根,则③④不成立,故只有②恒成立,从而得到结论.
解答:解:若两个根α、β 都为实根,则①不成立,②③④成立.
若两个根α、β 都为虚根,则③④不成立,①②成立.
综上,只有②恒成立,
故选A.
若两个根α、β 都为虚根,则③④不成立,①②成立.
综上,只有②恒成立,
故选A.
点评:本题考查关于x的实系数一元二次方程在复数集中根的分布与系数的关系,体现了分类讨论的数学思想.

练习册系列答案
相关题目
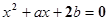 的一根在
的一根在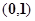 内,另一根在
内,另一根在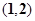 内,则点
内,则点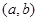 所在区域的面积为
所在区域的面积为 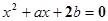 的一根在
的一根在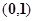 内,另一根在
内,另一根在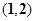 内,则点
内,则点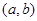 所在区域的面积为
所在区域的面积为