题目内容
20．设M为平行四边形ABCD的对角线的交点，O为平行四边形ABCD所在平面内任意一点，则$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$+$\overrightarrow{OD}$=$4\overrightarrow{OM}$．分析 由题意画出图象，判断出点M是对角线的中点，再由向量的平行四边形法则求出$\overrightarrow{OA}+\overrightarrow{OC}$和$\overrightarrow{OB}+\overrightarrow{OD}$，即可得到答案．
解答 解：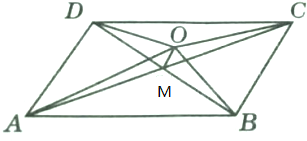
由平行四边形的性质可得：点M是对角线的中点，
∴$\overrightarrow{OA}+\overrightarrow{OC}$=$2\overrightarrow{OM}$，$\overrightarrow{OB}+\overrightarrow{OD}$=$2\overrightarrow{OM}$，
∴$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$+$\overrightarrow{OD}$=$4\overrightarrow{OM}$，
故答案为：$4\overrightarrow{OM}$．
点评 本题考查了向量的平行四边形法则，属于基础题．
练习册系列答案
相关题目
8．已知直线l1：y=-$\frac{1}{3}$ax-$\frac{1}{3}$，l2：y=-$\frac{2}{a+1}$x-$\frac{1}{a+1}$，若l1∥l2，则实数a的值是（ ）
| A． | a=-3或a=2 | B． | a=-3 | C． | a=-2 | D． | a=3 |
5．
如图是一个由圆、三角形、矩形组成的组合图，现用红黄两种颜色为其涂色，每个图形只涂一色，则三个颜色不全相同的概率是（ ）
如图是一个由圆、三角形、矩形组成的组合图，现用红黄两种颜色为其涂色，每个图形只涂一色，则三个颜色不全相同的概率是（ ）| A． | $\frac{1}{8}$ | B． | $\frac{3}{8}$ | C． | $\frac{1}{4}$ | D． | $\frac{3}{4}$ |