题目内容
已知圆C过点(1,0),且圆心在x轴的正半轴上,直线l:y=x-1被圆C所截得的弦长为2
.
(1)求过圆心且与直线l垂直的直线m方程;
(2)点P在直线m上,求以A(-1,0),B(1,0)为焦点且过P点的长轴长最小的椭圆的方程.
| 2 |
(1)求过圆心且与直线l垂直的直线m方程;
(2)点P在直线m上,求以A(-1,0),B(1,0)为焦点且过P点的长轴长最小的椭圆的方程.
分析:(1)先确定圆的圆心坐标,再根据直线l:y=x-1确定直线的斜率,从而可求过圆心且与直线l垂直的直线m方程;
(2)设B关于直线m对称的点的坐标为Q(3,2),则|PB|=|PQ|,故|PA|+|PB|=|PA|+|PQ|≥|AQ|,从而可求以A(-1,0),B(1,0)为焦点且过P点的长轴长最小的椭圆的方程.
(2)设B关于直线m对称的点的坐标为Q(3,2),则|PB|=|PQ|,故|PA|+|PB|=|PA|+|PQ|≥|AQ|,从而可求以A(-1,0),B(1,0)为焦点且过P点的长轴长最小的椭圆的方程.
解答: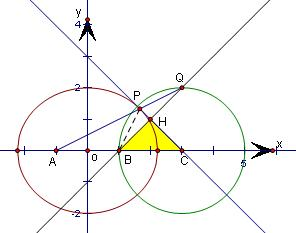 解:(1)根据题意画出图形,如图所示,
解:(1)根据题意画出图形,如图所示,
直线l:y=x-1被圆C所截得的弦的端点分别为B,Q,
设弦BQ的中点为H,在直角三角形BCH中,∠HBC=45°,|BH|=
|BQ|=
,
∴|BC|=2,即圆C的半径为2,
∴圆心C的坐标为(3,0),
∴过圆心且与直线l垂直的直线m方程为:y=-(x-3),即x+y-3=0.
(2)设B关于直线m对称的点的坐标为Q(x,y)
∴
,∴
∴Q(3,2),则|PB|=|PQ|,故|PA|+|PB|=|PA|+|PQ|≥|AQ|=2
,
设椭圆方程为
+
=1(a>b>0)
∴2a=2
,2c=2
∴b2=4
∵椭圆方程为
+
=1
 解:(1)根据题意画出图形,如图所示,
解:(1)根据题意画出图形,如图所示,直线l:y=x-1被圆C所截得的弦的端点分别为B,Q,
设弦BQ的中点为H,在直角三角形BCH中,∠HBC=45°,|BH|=
| 1 |
| 2 |
| 2 |
∴|BC|=2,即圆C的半径为2,
∴圆心C的坐标为(3,0),
∴过圆心且与直线l垂直的直线m方程为:y=-(x-3),即x+y-3=0.
(2)设B关于直线m对称的点的坐标为Q(x,y)
∴
|
|
∴Q(3,2),则|PB|=|PQ|,故|PA|+|PB|=|PA|+|PQ|≥|AQ|=2
| 5 |
设椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
∴2a=2
| 5 |
∴b2=4
∵椭圆方程为
| x2 |
| 5 |
| y2 |
| 4 |
点评:本题重点考查直线与椭圆的方程,考查点关于直线的对称问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目