题目内容
已知a=(cos ,sin
,sin ),b=(cos
),b=(cos ,sin
,sin )(0<
)(0< <
< <
<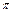 ).
).
(1)求证:a+b与a-b互相垂直;
(2)若ka+b与a-kb的模相等,求 -
- .(其中k为非零实数)
.(其中k为非零实数)
 ,sin
,sin ),b=(cos
),b=(cos ,sin
,sin )(0<
)(0< <
< <
<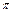 ).
).(1)求证:a+b与a-b互相垂直;
(2)若ka+b与a-kb的模相等,求
 -
- .(其中k为非零实数)
.(其中k为非零实数)(1)证明见解析(2) -
- =
=
 -
- =
=
(1)证明 (a+b)·(a-b)=a2-b2=|a|2-|b|2
=(cos2 +sin2
+sin2 )-(cos2
)-(cos2 +sin2
+sin2 )=0,
)=0,
∴a+b与a-b互相垂直.
(2)解 ka+b=(kcos +cos
+cos ,ksin
,ksin +sin
+sin ),a-kb=(cos
),a-kb=(cos -kcos
-kcos ,sin
,sin -ksin
-ksin ),
),
 =
=
 =
=

 =
= ,
,

又k 0,
0, cos(
cos( )=0.
)=0.
而0< <
< <
<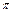 ,
,
 -
- =
= .
.
=(cos2
 +sin2
+sin2 )-(cos2
)-(cos2 +sin2
+sin2 )=0,
)=0,∴a+b与a-b互相垂直.
(2)解 ka+b=(kcos
 +cos
+cos ,ksin
,ksin +sin
+sin ),a-kb=(cos
),a-kb=(cos -kcos
-kcos ,sin
,sin -ksin
-ksin ),
), =
=
 =
=

 =
= ,
,
又k
 0,
0, cos(
cos( )=0.
)=0.而0<
 <
< <
<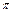 ,
,
 -
- =
= .
.
练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 ,
, ,若
,若 ∥
∥ ,则锐角
,则锐角 等于( )
等于( )



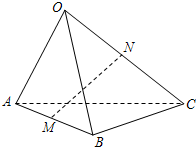
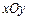 中,点
中,点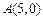 对于某个正实数
对于某个正实数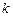 ,存在函数
,存在函数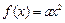 (
(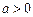 ),使得
),使得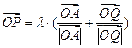 (
(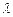 为常数),这里点
为常数),这里点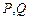 的坐标分别为
的坐标分别为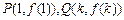 ,则
,则
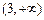
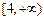

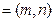 ,b
,b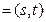 ,定义两个向量a,b之间的运算“
,定义两个向量a,b之间的运算“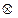 ”为
”为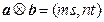 . 若向量p
. 若向量p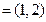 ,
,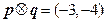 ,则向量q等于
,则向量q等于



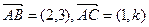 ,则实数
,则实数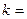 _____________。
_____________。 围绕原点按逆时针旋转
围绕原点按逆时针旋转 得到向量
得到向量 ,则
,则 ( )
( ) .
. B.
B. C.
C. D.
D.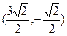
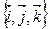
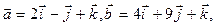
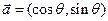 ,向量
,向量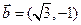 ,则
,则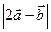 的最大值是 .
的最大值是 .