题目内容
两个变量x,y与其线性相关系数r有下列说法
(1)若r>0,则x增大时,y也相应增大; (2)若r<0,则x增大时,y也相应增大;
(3)若r=1或r=-1,则x与y的关系完全对应( 有函数关系),在散点图上各个散点均在一条直线上.其中正确的有( )
| A.① | B.②③ | C.①③ | D.①②③ |
C
解析试题分析:r>0时,说明x,y正相关,所以“(1)若r>0,则x增大时,y也相应增大”正确;
r<0时,说明x,y负相关,所以“(2)若r<0,则x增大时,y也相应增大”不正确;
r=1或r=-1,说明x与y具有函数关系,所以“(3)若r=1或r=-1,则x与y的关系完全对应( 有函数关系),在散点图上各个散点均在一条直线上.”正确,故选C。
考点:本题主要考查两个变量x,y与其线性相关系数r的概念及其关系。
点评:简单题,关键是理解相应概念及关系。

练习册系列答案
相关题目
在两个变量y与x的回归模型中,分别选择了4个不同模型,它们的相关指数R2如下,其中拟和效果最好的模型是( )
| A.模型1的相关指数R2为0.25 | B.模型2的相关指数R2为0.50 |
| C.模型3的相关指数R2为0.98 | D.模型4的相关指数R2为0.80 |
从2003件产品中选取50件,若采用下面的方法选取:先用简单随机抽样从2003件产品中剔除3件,剩下的2000件再按系统抽样的方法抽取,则每件产品被选中的概率
| A.不都相等 | B.都不相等 | C.都相等,且为 | D.都相等,且为 |
以下有关线性回归分析的说法不正确的是( )
A.通过最小二乘法得到的线性回归直线经过样本的中心 |
B.用最小二乘法求回归直线方程,是寻求使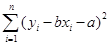 最小的a,b的值 最小的a,b的值 |
| C.相关系数r越小,表明两个变量相关性越弱 |
D. 越接近1,表明回归的效果越好 越接近1,表明回归的效果越好 |
已知二次函数 的x与y的部分对应值如下表:
的x与y的部分对应值如下表:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 11 | | 1 | -1 | -1 | 1 | 5 |
 的两根分别为
的两根分别为 、
、 ,下面说法错误的是( ) .
,下面说法错误的是( ) .A.
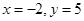 B.
B.
C.当
 时,
时,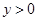 D.当
D.当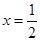 时,
时, 有最小值
有最小值 在建立两个变量 与
与 的回归模型中,分别选择了4个不同的模型,它们的相关指数
的回归模型中,分别选择了4个不同的模型,它们的相关指数 如下,其中拟合最好的模型是( )
如下,其中拟合最好的模型是( )
A.模型1的相关指数 为0.98 为0.98 | B.模型2的相关指数 为0.80 为0.80 |
C.模型3的相关指数 为0.50 为0.50 | D.模型4的相关指数 为0.25 为0.25 |
对变量 有观测数据(
有观测数据( ,
, )(
)( ),得散点图1;对变量
),得散点图1;对变量 有观测数据(
有观测数据( ,
, )(i=1,2,…,10),得散点图2. 由这两个散点图可以判断
)(i=1,2,…,10),得散点图2. 由这两个散点图可以判断
| A.变量x 与y 正相关,u 与v 正相关 | B.变量x 与y 正相关,u 与v 负相关 |
| C.变量x 与y 负相关,u 与v 正相关 | D.变量x 与y 负相关,u 与v 负相关 |
设(x1,y1),(x2,y2),…,(xn,yn),是变量x:和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归方程(如图),以下结论中正确的是
| A. x;和y正相关 |
| B. x和y的相关系数为直线l的斜率 |
| C. x和y的相关系数在-1到0之间 |
| D.当n为偶数时,分布在l两侧的样本点的个数一定相同 |


 的值为( )
的值为( )