题目内容
【题目】将一个水族箱用屏障在中间隔成A、B两部分,然后在A、B两侧分别放入数量相同的少量水蚤(小型甲壳动物)和草履虫,给予充足的食物,并满足其他生活条件,观察它们的生长。h小时后,两个种群的个体数量都发展到环境条件所允许的最大值(即K值)时,继续供给草履虫食物,但不再供给水蚤食物,并把屏障撤掉。请分析回答:
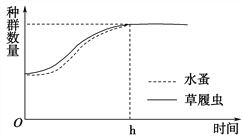
(1)在O~h小时内,两个种群的增长均呈__________型曲线。
(2)达到K值时,种群数量不再增加的主要原因是____________________________。
(3)在h小时后,草履虫数量逐渐减少,引起这一变化的主要生物因素是____________。
(4)在坐标图中绘出h小时后两个种群数量变化的曲线。__________
【答案】 “S” 空间的限制 水蚤的捕食 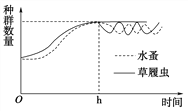
【解析】本题考查种群数量变化及种间关系,要求考生理解种群数量变化的“S”型曲线形成过程,理解K值的含义及其应用,能根据题意判断出题给的草履虫和水蚤之间种间关系,进而画出相关的坐标曲线。
(1)在O~h小时内,由于水蚤和草履虫都在固定的生活空间中,所以随着种群数量的增加,生活空间不足,两个种群的增长均呈现出“S”型曲线。
(2)达到K值时,种群数量不再增加的主要原因是生存空间的限制。
(3)根据题意,在h小时后,继续供给草履虫食物,但不再供给水蚤食物,并把屏障撤掉,则会由于水蚤的捕食,导致草履虫数量逐渐减少。
(4)根据题干中“h小时后,供给草履虫食物,但不再供给水蚤食物,并把屏障撤掉”,水蚤就会以草履虫为食物,出现捕食关系的曲线,可表示为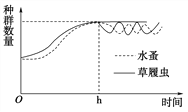 。
。

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案【题目】某人承包了一个鱼塘,放养了2000尾鲫鱼,在最初4个月内,由于资源和空间充足,每个月鱼的数量是上一个月的2倍。请回答下列问题:
(1)为了研究鱼的生长发育及繁殖情况,设计了如下建立数学模型的步骤:
鱼的情况 | 研究方法 |
鱼的数量每一个月是上一个月的2倍 | ① |
4个月内池塘的资源和空间充足,鱼的增长不受鱼的密度增加的影响 | ② |
③ | 根据实验数据,用适当的数学形式对事物的性质进行表达 |
观察统计鱼的数量,对自己所建立的模型进行检验或修正 | 通过进一步实验或观察等,对模型进行检验或修正 |
请对该步骤进行补充,即写出上表中①②③处的内容。
(2)假设该池塘最多能够容纳5万尾鲫鱼生长,则在捕捞时,应让池塘保持________尾鲫鱼时能发挥最大经济效率。
(3)在调查鱼的种群密度时,常用的估算方法是______,此方法是否适宜作为土壤动物调查的估算方法?________。理由是________________________。
【题目】南方某地的常绿阔叶林曾因过度砍伐而遭到破坏。停止砍伐一段时间后,该地常绿阔叶林逐步得到恢复,下表为恢复过程依次更替的群落类型及其植物组成。在由下表种群落构成的相应生态系统中,抵抗力稳定性最强的是( )
演替阶段 | 群落类型 | 植物种数/种 | ||
草本植物 | 灌木 | 乔木 | ||
1 | 草丛 | 34 | 0 | 0 |
2 | 针叶林 | 52 | 12 | 1 |
3 | 针阔叶混交林 | 67 | 24 | 17 |
4 | 常绿阔叶林 | 106 | 31 | 16 |
A. 草丛 B. 针叶林
C. 针阔叶混交林 D. 常绿阔叶林