题目内容
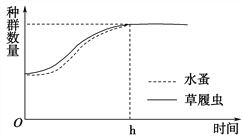
【题目】某人承包了一个鱼塘,放养了2000尾鲫鱼,在最初4个月内,由于资源和空间充足,每个月鱼的数量是上一个月的2倍。请回答下列问题:
(1)为了研究鱼的生长发育及繁殖情况,设计了如下建立数学模型的步骤:
鱼的情况 | 研究方法 |
鱼的数量每一个月是上一个月的2倍 | ① |
4个月内池塘的资源和空间充足,鱼的增长不受鱼的密度增加的影响 | ② |
③ | 根据实验数据,用适当的数学形式对事物的性质进行表达 |
观察统计鱼的数量,对自己所建立的模型进行检验或修正 | 通过进一步实验或观察等,对模型进行检验或修正 |
请对该步骤进行补充,即写出上表中①②③处的内容。
(2)假设该池塘最多能够容纳5万尾鲫鱼生长,则在捕捞时,应让池塘保持________尾鲫鱼时能发挥最大经济效率。
(3)在调查鱼的种群密度时,常用的估算方法是______,此方法是否适宜作为土壤动物调查的估算方法?________。理由是________________________。
【答案】 ①观察研究对象,提出问题 ②提出合理的假设 ③Nt=N0·λt(其中,Nt代表t个月后鱼的数量,t表示时间,λ表示倍数,N0表示最初的鱼的数量) 25000 标志重捕法 不适宜 大多数土壤动物身体微小,活动范围小,标记个体难与无标记个体充分混匀
【解析】本题考查数学模型的构建方法、种群数量变化及种群密度的调查,要求考生理解构建数学模型的一般步骤,理解种群数量变化的“S”型曲线及其应用,掌握不同生物种群密度的调查方法。
(1)数学模型是用来描述一个系统或它的性质的数学形式,
其研究方法一般是:①观察研究对象,提出问题→②提出合理的假设→③根据实验数据,用适当的数学形式对事物的性质进行表达→④通过进一步实验或观察等,对模型进行检验或修正;要研究鱼的生长发育及繁殖情况,可设计建立数学模型的步骤为:①了解鱼的情况,提出问题→②提出“鱼的数量每一个月是上一个月的2倍”合理的假设→③根据实验数据,用适当的数学形式对事物的性质进行表达,即Nt=N0·λt(其中,Nt代表t个月后鱼的数量,t表示时间,λ表示倍数,N0表示最初的鱼的数量)→④观察统计鱼的数量,对自己所建立的模型进行检验或修正。
(2)假设该池塘最多能够容纳5万尾鲫鱼生长,即种群的K值为5万尾;种群数量在K/2时增长速率最大,则在捕捞时,应让池塘保持5万尾![]() = 25000尾鲫鱼时能发挥最大经济效率。
= 25000尾鲫鱼时能发挥最大经济效率。
(3)鱼的活动能力强、活动范围大,故调查鱼的种群密度时,常用的估算方法是标志重捕法;由于大多数土壤动物身体微小,活动范围小,标记个体难与无标记个体充分混匀,因此不能用标志重捕法作为土壤动物调查的估算方法,土壤动物的调查一般用取样器取样法。
野生生物资源的保护与利用 | 有害生物的防治 | |
K值(环境最大容纳量) | 保护野生生物生活的环境,减小环境阻力,增大K值 | 增大环境阻力(如为防鼠害而封锁粮食、清除生活垃圾、保护鼠的天敌等),降低K值 |
K/2(最大增长速率) | 捕捞后,使鱼的种群数量维持在K/2,鱼的种群数量会迅速回升 | 务必及时控制种群数量,严防达K/2值处(若达K/2值处,可导致该有害生物成灾) |