题目内容
【题目】下面是一些晶体的结构示意图。请回答下列问题:
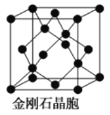
(1)下图为金刚石晶胞,则1个金刚石晶胞含有_________个碳原子。若碳原子半径为r,金刚石晶胞的边长为a,根据硬球接触模型,则r=_________a。
(2)下图为钛酸钡晶体的晶胞结构,该晶体经X—射线分析得出,重复单位为立方体,顶点位置被Ti4+所占据,体心位置被Ba2+所占据,棱心位置被O2-所占据。
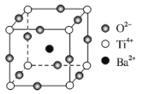
①在该物质的晶体中,每个Ti4+周围与它距离最近且相等的Ti4+有_____个,它们的空间构型为_____。O2-的钡配位数是______。
②若将Ti4+置于晶胞的体心,Ba2+置于晶胞顶点,则O2-处于立方体的______位置。
(3)PbS是一种重要的半导体材料,具有NaCl型结构(如下图),其中阴离子采用面心立方最密堆积方式,X—射线衍射实验测得PbS的晶胞参数为a=0.594nm。

①已知坐标参数:A(0,0,0),B(![]() ,
,![]() ,0),则C 的坐标参数为 ________ 。
,0),则C 的坐标参数为 ________ 。
②PbS晶体的密度为______ gcm-3。(列出计算式即可)
【答案】8 ![]() 6 正八面体 4 面心 (
6 正八面体 4 面心 (![]() ,
,![]() ,
,![]() )
) ![]()
【解析】
(1)利用均摊法计算;
(2)①晶胞顶点位置上的Ti4+与其上、下、左、右、前、后的6个Ti4+最邻近且距离相等;以棱上的O2-为参照点,与O2-最邻近且距离相等的Ba2+位于每个晶胞的体心;
②若将Ti4+置于晶胞的体心,Ba2+置于晶胞顶点,则O2-处于立方体的面心;
(3)①由A、B坐标参数,可知A为坐标系原点,坐标系面xOy为晶胞下底面,坐标系面xOz为晶胞左侧面,坐标系面yOz为晶胞后平面,C为位于晶胞体心,到各面的距离相等;
②均摊法计算晶胞中Pb2+、S2离子数目,计算晶胞中离子总质量,晶体密度=晶胞质量÷晶胞体积。
(1)晶胞中顶点微粒数为:8×![]() =1,面心微粒数为:6×
=1,面心微粒数为:6×![]() =3,体内微粒数为4,共含有8个碳原子;位于晶胞内部的四个碳原子处于八分之一晶胞的中心,因此,晶胞的体对角线长度与四个碳原子直径相同,即
=3,体内微粒数为4,共含有8个碳原子;位于晶胞内部的四个碳原子处于八分之一晶胞的中心,因此,晶胞的体对角线长度与四个碳原子直径相同,即![]() a=8r,r=
a=8r,r=![]() a;
a;
(2)①由晶体结构,晶胞顶点位置上的Ti4+与其上、下、左、右、前、后的6个Ti4+最邻近且距离相等;若将它们连接起来,则形成一个正八面体;每个晶胞含有一个Ba2+,O2-位于晶胞的棱上,被4个晶胞共用,与它最邻近且距离相等的Ba2+位于晶胞的体心,则O2-的钡配位数是4;
②根据晶胞结构可知,每个Ti4+周围有6个O2-,若Ti4+位于晶胞的体心,Ba2+位于晶胞的顶点,则O2-处于立方体面心上;
(3)①由A、B坐标参数,可知A为坐标系原点,坐标系面xOy为晶胞下底面,坐标系面xOz为晶胞左侧面,坐标系面yOz为晶胞后平面,C为位于晶胞体心,到各面的距离相等,结合B(![]() ,
,![]() ,0),则C的坐标参数为(
,0),则C的坐标参数为(![]() ,
,![]() ,
,![]() );
);
②晶胞中Pb2+离子数目=1+12×![]() =4、S2离子数目=8×
=4、S2离子数目=8×![]() +6×
+6×![]() =4,晶胞中离子总质量=
=4,晶胞中离子总质量=![]() g,晶体密度=
g,晶体密度=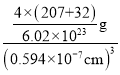 =
=![]() g/cm3。
g/cm3。