题目内容
14.第四周期过渡金属及其化合物在合金材料以及催化剂等方面应用广泛.请回答下列问题:(1)镍在周期表中的位置第四周期第Ⅷ族,Fe2+的价电子有6种不同运动状态的电子.
(2)NiO、FeO的晶体结构类型均与氯化钠的相同,Ni2+和Fe2+的离子半径分别为69pm和78pm,则熔点FeO<NiO (填“<”或“>”),解释原因NiO和FeO均为离子晶体,它们的阴阳离子所带电荷均相同,但Ni2+半径小,因而NiO晶体晶格能大,所以熔沸点高于FeO;
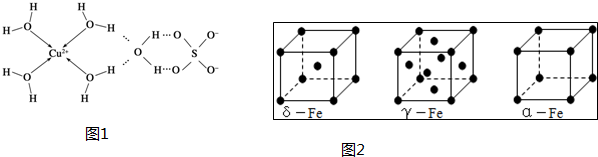
(3)通过X射线推测胆矾中既含有配位键,又含有氢键,其结构示意图可简单表示如图1:
①矾的化学式用配合物的形式表示为[Cu(H2O)4]SO4•H2O.
②实验测得冰中氢键的作用力为18.5kJ/mol,而冰的熔化热为5.0kJ/mol,这说明氢键没有完全被破坏;
(4)铁有δ、γ、α三种同素异形体,各晶胞如图2:
①则δ、γ、α三种晶胞中铁原子的配位数之比为4:6:3.
②设α-Fe晶胞边长为a cm,δ-Fe晶胞边长为b cm,计算确定α-Fe和δ-Fe两种晶体的密度比为:b3:2a3.(用a、b的代数式表示)
③如已知γ型晶体铁的密度为ag/cm3,铁的摩尔质量为bg/mol,则铁原子的半径r=$\frac{\sqrt{2}}{4}$×$\root{3}{\frac{4b}{a{N}_{A}}}$cm(列式计算,NA表示阿伏伽德罗常数值)
分析 (1)镍在周期表中的位置:第四周期第Ⅷ族,Fe2+的价电子排布式为3d6;
(2)离子所带电荷相同,阴离子均为氧离子,阳离子离子半径越大,晶格能越小,熔点越低;
(3)①Cu2+与水分子之间形成配位键,硫酸根与水分子之间形成氢键,配离子之间通过氢键理解;
②实验测得冰中氢键的作用力为18.5kJ/mol,而冰的熔化热为5.0kJ/mol,说明氢键没有完全破坏;
(4)①δ-Fe为体心立方密堆积,配位数为8,γ-Fe为面心立方密堆积,配位数为12,α=Fe为简单立方堆积,配位数为6;
②利用均摊法计算晶胞中Fe原子数目,进而计算晶胞质量,根据ρ=$\frac{m}{V}$计算晶胞密度;
③利用均摊法计算晶胞中Fe原子数目,进而计算晶胞质量,根据V=$\frac{m}{ρ}$计算晶胞体积,晶胞棱长=$\root{3}{V}$,处于面对角线上的原子相邻,则4r=$\root{3}{V}$×$\sqrt{2}$.
解答 解:(1)镍在周期表中的位置:第四周期第Ⅷ族,Fe2+的价电子排布式为3d6,价电子有6种不同运动状态的电子,故答案为:第四周期第Ⅷ族;6;
(2)NiO和FeO均为离子晶体,它们的阴阳离子所带电荷均相同,但Ni2+半径小,因而NiO晶体晶格能大,所以熔沸点高于FeO,
故答案为:<;NiO和FeO均为离子晶体,它们的阴阳离子所带电荷均相同,但Ni2+半径小,因而NiO晶体晶格能大,所以熔沸点高于FeO;
(3)①Cu2+与水分子之间形成配位键,硫酸根与水分子之间形成氢键,配离子之间通过氢键理解,胆矾的化学式为:[Cu(H2O)4]SO4•H2O,故答案为:[Cu(H2O)4]SO4•H2O;
②实验测得冰中氢键的作用力为18.5kJ/mol,而冰的熔化热为5.0kJ/mol,说明氢键没有完全破坏,故答案为:氢键没有完全被破坏;
(4)①δ-Fe为体心立方密堆积,配位数为8,γ-Fe为面心立方密堆积,配位数为12,α=Fe为简单立方堆积,配位数为6,则δ、γ、α三种晶胞中铁原子的配位数之比为8:12:6=4:6:3,故答案为:4:6:3;
②设α-Fe晶胞边长为a cm,体积为(a cm)3,晶胞中Fe原子数目为8×$\frac{1}{8}$=1,晶胞质量为$\frac{56}{{N}_{A}}$g,故晶体密度为$\frac{56}{{N}_{A}}$g÷(a cm)3=$\frac{56}{{a}^{3}{N}_{A}}$g/cm3,
δ-Fe晶胞边长为b cm,体积为(b cm)3,晶胞中Fe原子数目为1+8×$\frac{1}{8}$=2,晶胞质量为$\frac{2×56}{{N}_{A}}$g,故晶体密度为为$\frac{2×56}{{N}_{A}}$g÷(b cm)3=$\frac{2×56}{{b}^{3}{N}_{A}}$g/cm3,
则α-Fe和δ-Fe两种晶体的密度比为 $\frac{56}{{a}^{3}{N}_{A}}$g/cm3:$\frac{2×56}{{b}^{3}{N}_{A}}$g/cm3=b3:2a3,
故答案为:b3:2a3;
③γ型晶体铁晶胞中Fe原子数目为6×$\frac{1}{2}$+8×$\frac{1}{8}$=4,晶胞质量为$\frac{4×b}{{N}_{A}}$g,γ型晶体铁的密度为ag/cm3,晶胞体积为$\frac{4×b}{{N}_{A}}$g÷ag/cm3=$\frac{4b}{a{N}_{A}}$cm3,则晶胞棱长=$\root{3}{\frac{4b}{a{N}_{A}}}$cm,处于面对角线上的原子相邻,则4r=$\root{3}{\frac{4b}{a{N}_{A}}}$cm×$\sqrt{2}$,故r=$\frac{\sqrt{2}}{4}$×$\root{3}{\frac{4b}{a{N}_{A}}}$cm,
故答案为:$\frac{\sqrt{2}}{4}$×$\root{3}{\frac{4b}{a{N}_{A}}}$.
点评 本题是对物质结构的考查,涉及核外电子排布、晶体类型与性质、配合物、氢键、晶胞计算等,需要学生具备扎实的基础与一定的数学计算能力,难度中等.

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案| 选项 | 化学反应及其离子方程式 | 评 价 |
| A | NaHSO4溶液与Ba(OH)2溶液反应至 SO42-沉淀完全: 2H++SO42-+Ba2++2OH-=BaSO4↓+2H2O | 正 确 |
| B | 向碳酸镁溶液中加入足量稀盐酸: CO32-+2H+=CO2↑+H2O | 错误,碳酸镁不应写成离子形式 |
| C | 向沸水中滴加饱和的氯化铁溶液至液体变为红褐色: Fe3++3H2O=Fe(OH)3↓+3H+ | 正 确 |
| D | NaOH溶液中通入少量CO2反应:OH-+CO2=HCO3- | 正 确 |
| A. | A | B. | B | C. | C | D. | D |
| A. | 物质的熔点:石英>食盐>冰 | |
| B. | 热稳定性:H2O>HI>HBr>HCl | |
| C. | 分散系中分散质粒子的直径:Fe(OH)3悬浊液>Fe(OH)3胶体>FeCl3溶液 | |
| D. | 微粒的半径:Cl->Na+>Mg2+>Al3+ |
| A. | 钠保存在细口瓶中,并加煤油液封 | |
| B. | 氯水保存在棕色瓶中,并置于冷暗处 | |
| C. | Na2CO3溶液保存在无色瓶中,塞橡皮塞 | |
| D. | 工业上将Cl2贮存在钢瓶中 |
| A. | 是一种无色无味的气体 | B. | 遇水蒸气会形成白雾 | ||
| C. | 和水反应生成两种酸 | D. | 具有漂白性 |
| A. | 布朗运动是胶体特有的运动方式,只用肉眼就可以区别开胶体、浊液和溶液 | |
| B. | 向Fe(OH)3胶体中加入过量的稀硫酸,最终使胶体发生聚沉形成沉淀物 | |
| C. | 一般的,胶体微粒具有较大的表面积,能吸附某些离子而带电荷,故在电场作用下会产生电泳现象 | |
| D. | 胶体不稳定,静置后容易产生沉淀 |
| A. | 1 mol•L-1 HCl溶液:c(Cl-)>c(H+)>c(OH-) | |
| B. | 1 mol•L-1 Na2CO3溶液:c(Na+)+c(H+)=2c(CO32-)+c(HCO3-)+c(OH-) | |
| C. | 1 mol•L-1 NaHCO3溶液:c(H+)+2c(H2CO3)=c(OH-)+c(CO32-) | |
| D. | 0.1 mol•L-1NaOH溶液与等体积pH=1的醋酸混合后的溶液中:c (CH3COO-)=c (Na+)>c (H+)=c (OH-) |