题目内容
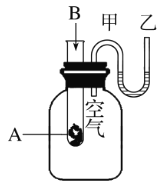
【题目】科学家研究出一种以天然气为燃料的“燃烧前捕获系统”,其简单流程如图所示(条件及物质未标出)。

(1)已知:CH4、CO、H2的燃烧热分别为890.3 kJ·mol-1、283.0 kJ·mol-1、285.8 kJ·mol-1,则上述流程中第一步反应2CH4(g)+O2(g)===2CO(g)+4H2(g)的ΔH=____________。
(2)\在300 ℃、8 MPa下,将CO2和H2按物质的量之比1∶3 通入一密闭容器中发生反应CO2(g)+3H2(g)![]() CH3OH(g)+H2O(g),,达到平衡时,测得CO2的平衡转化率为50%,则该反应条件下的平衡常数表达式为K=________
CH3OH(g)+H2O(g),,达到平衡时,测得CO2的平衡转化率为50%,则该反应条件下的平衡常数表达式为K=________
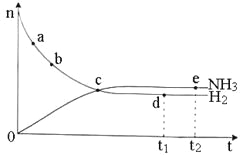
(3)CO2经催化加氢可合成低碳烯烃:2CO2(g)+6H2(g)![]() C2H4(g)+4H2O(g) ΔH。在0.1 MPa时,按n(CO2)∶n(H2)=1∶3投料,如图所示为不同温度(T)下,平衡时四种气态物质的物质的量(n)关系。
C2H4(g)+4H2O(g) ΔH。在0.1 MPa时,按n(CO2)∶n(H2)=1∶3投料,如图所示为不同温度(T)下,平衡时四种气态物质的物质的量(n)关系。
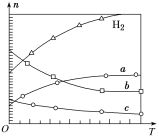
①该反应的ΔH________0(填“>”或“<”)。
②曲线c表示的物质为________。
③为提高H2的平衡转化率,除改变温度外,还可采取的措施是_________________。
【答案】-71.4 kJ·mol-1 ![]() < C2H4 加压(或不断分离出水蒸气)
< C2H4 加压(或不断分离出水蒸气)
【解析】
(1)根据CH4、H2、和CO的燃烧热分别写出燃烧的热化学方程式,利用盖斯定律书写该反应的热化学方程式;
(2)依据平衡常数概念写出,用生成物平衡浓度幂次方乘积除以反应物平衡浓度的幂次方乘积得到平衡常数表达式;
(3)由曲线氢气的变化,确定反应放热还是吸热;随着温度升高,氢气的物质的量逐渐增多,因氢气为反应物,则另一条逐渐增多的曲线为CO2,由计量数关系确定b、c;根据压强或浓度对平衡的影响判断。
(1)已知:①CH4(g)+2O2(g)=CO2(g)+2H2O(l) △H=-890.3 kJ·mol-1;②CO(g)+![]() O2(g)=CO2(g)△H=-283.0 kJ·mol-1 ;③H2(g)+
O2(g)=CO2(g)△H=-283.0 kJ·mol-1 ;③H2(g)+![]() O2(g)=H2O(l)△H=-285.8 kJ·mol-1,根据盖斯定律2×①-②×2-③×4得2CH4(g)+O2(g)=2CO(g)+4H2(g) ΔH=-71.4 kJ·mol-1;
O2(g)=H2O(l)△H=-285.8 kJ·mol-1,根据盖斯定律2×①-②×2-③×4得2CH4(g)+O2(g)=2CO(g)+4H2(g) ΔH=-71.4 kJ·mol-1;
(2)依据平衡常数概念写出,用生成物平衡浓度幂次方乘积除以反应物平衡浓度的幂次方乘积得到平衡常数表达式;则该反应条件下的平衡常数表达式为K=![]() ;
;
(3)由曲线变化可知随着温度升高,氢气的物质的量逐渐增多,说明升高温度平衡逆向移动,则正反应放热,故△H<O;随着温度升高,氢气的物质的量逐渐增多,因氢气为反应物,则另一条逐渐增多的曲线为CO2,由计量数关系可知b为水,c为C2H4的变化曲线;正反应是体积减小的放热反应,则提高氢气的转化率可以采用加压(或不断分离出水蒸气)的方法。