题目内容
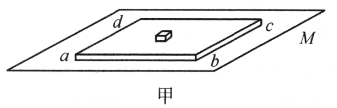
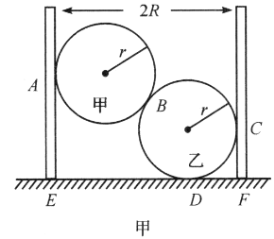
【题目】质量均匀的无底圆桶重![]() ,放在水平桌面上,如图甲所示,内放甲、乙均匀圆球,每球重为
,放在水平桌面上,如图甲所示,内放甲、乙均匀圆球,每球重为![]() 、半径为
、半径为![]() ,桶的半径为
,桶的半径为![]() ,且
,且![]() ,若各接触面间摩擦不计,试求为使圆桶不至于翻倒
,若各接触面间摩擦不计,试求为使圆桶不至于翻倒![]() 的最小值。如果桶有底呢?
的最小值。如果桶有底呢?
【答案】![]() ,如果桶有底,桶不可能翻倒。
,如果桶有底,桶不可能翻倒。
【解析】
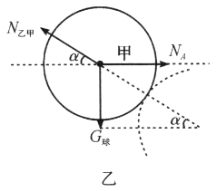
方法1 小球甲受到三个力:重力![]() 、桶壁的支持力
、桶壁的支持力![]() 和乙球对甲球的弹力
和乙球对甲球的弹力![]() (沿两球球心),如图乙所示。
(沿两球球心),如图乙所示。
根据平衡条件可得![]() ,
,![]() ,
,
解得![]() .
.
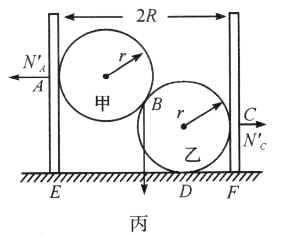
把甲、乙两个球作为一个整体,如图丙所示,由水平方向的平衡条件可知乙球在![]() 点受到的弹力
点受到的弹力![]() 。由牛顿第三定律可知,甲、乙两球对桶壁的弹力
。由牛顿第三定律可知,甲、乙两球对桶壁的弹力![]() 的大小分别等于
的大小分别等于![]() 。对无底圆桶,取
。对无底圆桶,取![]() 点为转动轴时,将要翻时,仅
点为转动轴时,将要翻时,仅![]() 处与对面有弹力,要使圆桶不致翻倒,由力矩平衡条件
处与对面有弹力,要使圆桶不致翻倒,由力矩平衡条件
![]() ,
,
从而,![]()
![]() .
.
如果桶有底,则整体分析,由受力可知地面对整个桶底总有弹力,因此桶不可能翻倒。
方法2 如图丁所示,把甲、乙两个球作为一个整体,由竖直方向受力平衡可知地面对球乙的弹力大小为![]() ,将两个球和桶作为整体分析,取
,将两个球和桶作为整体分析,取![]() 点为转动轴,将要翻时,仅
点为转动轴,将要翻时,仅![]() 处与地面有弹力。要使圆桶不致翻倒,由力矩平衡条件得
处与地面有弹力。要使圆桶不致翻倒,由力矩平衡条件得
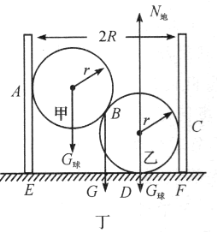
![]() ,
,
即![]() ,
,
解得![]() .
.
如果桶有底,则整体分析,由受力可知地面对整个桶底总有弹力,因此桶不可能翻倒。

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目