题目内容
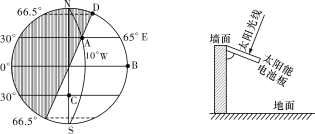
【题目】下左图为某日某时刻半球昼夜分布示意图,阴影为黑夜;下右图为太阳能电池板示意图。读图回答下列问题。
(1)该日的日期大约是__________。
(2)该时刻太阳直射的纬度是__________,B点的地方时为________。
(3)此时,B点旗杆影长为一天中______(填“最大”或“最小”)值,旗杆影子的方向为________。
(4)将该日A、B、C三地的正午太阳高度从大到小排序__________。
(5)该日A地体育场馆的太阳能电池板与建筑物外墙(墙面与地面垂直,见上右图)之间最合适的夹角约为________;若此夹角可以调节,那么其一年中的变化幅度(一年中最大夹角与最小夹角之差)约为__________。
【答案】12月22日 23.5°S 12:00 最小 正北 CBA 36.5° 47°
【解析】
本题以太阳光照图和太阳能热水器为载体,考查太阳直射点的位置、地方时、正午影长、影子方向、正午太阳高度的计算公式及应用,旨在考查学生的读图能力和综合思维能力。
(1)读左图可知,北极圈及其以北地区出现极夜,此日节气应为冬至,日期为12月22日前后。
(2)由上题分析可知,该日节气为冬至,太阳直射南回归线,即23.5°S。读图可知,太阳直射点的经度为65°E,65°E经线上的地方时为12时;因此,位于65°E经线上的B点的地方时也为12时。
(3)由上题分析可知,B点为正午时刻,B点旗杆影长为一天中的最短长度。由图可知,B点位于赤道,结合上题上题分析,此日太阳直射南回归线;故正午时刻太阳位于B点的正南方,B点旗杆影子朝向正北。
(4)由上述小题分析可知,此日太阳直射南回归线,即23.5°S。根据正午太阳高度计算公式分析,某地纬度与直射点纬度差值越小,该地的正午太阳高度则越大。图中A、B、C三点纬度与直射点纬度差值分别为53.5°、23.5、6.5°,因此,该日A、B、C三地正午太阳高度由大到小的排序为C、B、A。
(5)根据示意图中的几何关系判断,太阳能电池板与建筑物外墙之间最适合的夹角应等于该地正午太阳高度。由上题分析可知,该日A地纬度与直射点纬度差值为53.5°,故A地正午太阳高度为36.5°。因此,所求夹角约为36.5°。由题干可知,该夹角的变化幅度为一年中最大夹角与最小夹角之差,即该地一年中正午太阳高度的最大值与最小值之差。由图可知,A地纬度为30°N(北回归线以北地区),夏至日的正午太阳高度等于90°-(30°-23.5°),为一年中最大值,冬至日的正午太阳高度等于90°-(30°+23.5°),为一年中最小值;因此,该夹角的变化幅度为90°-(30°-23.5°)-[90°-(30°+23.5°)]=47°。