Question

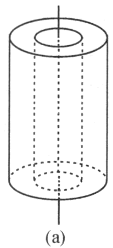
【题目】空气圆筒形电容器是两个共轴薄壁金属圆筒，如图a所示．每个圆筒长为l，半径分别为R和r，并且．电容器的电容为．如果两个圆筒半径增加一倍，而其长度减小到三分之一，求新电容器的电容．可以认为带电筒形电容器两极之间电场强度E与到轴距离x成反比例减小，即．

Answer 1

【答案】

【解析】

按定义，电容器的电容等于．为了求电容器的电容，需要使它“充电”任一电量q，且计算两极之间产生的电势差，按定义，有

式中W为在带电电容器两极之间移动检验电荷所做的功。

为了求功W，作出作用在检验电荷上电场力与距离x关系图像，如图b所示．

所求的功W为所有元功之和（图上直角柱子的面积）且数值等于画阴影的曲线梯形的面积．如果现在不改变电量，将R和r增加一倍，那么所做的功用面积表示，如图（c）所示．不难设想，（当保持分割方法且元直角柱子的总数目不变，每个这样的直角柱子沿x轴延长一倍且沿F轴缩短一半）．由此可见，当同时改变R和r同样倍数时，圆筒形电容器的电容不变。

电容器长度变化导致电容成比例地变化，因为这时在两极之间距离不变的情况下两极的面积发生变化．

因此，半径R和r增加一倍不改变电容器的电容，而长度l减小到三分之一，导致它的电容也减小到三分之一，即．