题目内容
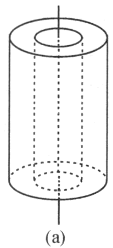
【题目】如图所示，在一光滑水平圆桌面上有两个质量、电荷都均匀分布的介质球，两球半径均为a，A球质量为m，所带电荷量为Q，B球质量为4m，所带电荷量为
．在初始时刻，两球球心距为4a，各有一定的初速度，以使得两球在以后的运动过程中不发生碰撞，且都不会从圆桌面掉落．现要求在此前提下尽量减小桌面面积，试求：
（1）两球初速度的方向和大小；
（2）圆桌面的最小半径．
假设两球在运动过程中，其所带电荷量始终保持均匀分布：桌面也不发生极化效应．已知两个均匀带电球之间的静电相互作用力，等于电荷集中在球心的两个点电荷之间的相互作用力；静电力常量为
．
【答案】（1）
，
（2）
【解析】
（1）（2）要使两小球在桌面上不掉下来，则两小球的质心在桌面上不能移动。
初始时刻，质心在两球球心的连线上，与A球球心和B球球心的距离分别是
，
在此后的运动中，两球的球心到质心的距离比保持不变．
依题意，两球之间的库仑力为
．
在质心系中，用
和
必分别表示质心到A球球心和B球球心方向上的单位矢量，则A、B两球的运动方程分别是
，
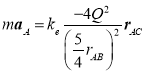上述两式表明，A、B两球在质心系中均做椭圆运动．
为了使两球的运动轨道覆盖尽量小的面积，球心距的初始值4a应该是它的最大值；而不相碰则表明其最小值应为2a，所以，初始时，A、B两球分别处于其椭圆轨道的远点，与质心的距离分别为
和
，A、B两球分别处于其椭圆轨道的近点时，易得与质心的距离分别为
和
。
由此可知：
A球椭圆轨道的半长轴和半短轴分别是
，
．
B球椭圆轨道的半长轴和半短轴分别是
由于质心不动，则任意时刻均有
，且方向相反。
由于初始时刻两球相距最远，则两球球心的速度必垂直于两球球心的连线，若设B球的初速度为
，则A球的初速度
；同理，当两球相距最近时，B球和A球的速度分别为
和
，方向亦垂直于两球球心连线．
由角动量守恒有
由此得
由能量守恒得
解得，
另外，由前面的分析计算可知，最小的圆桌面范围由A球的运动划定，在质心系中，它的轨道是以质心为力心、半长轴与半短轴分别为、
的椭圆，所以，两均不会从桌面上落下的圆桌面最小半径为
．
