题目内容
【题目】设赛车道在同一水平面上,车轮与地面间的摩擦因数为![]() ,且
,且![]() 不随速度变化,问:
不随速度变化,问:
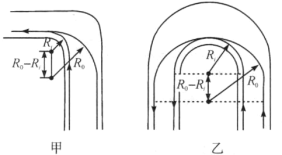
(1)当赛车运动员驾车做90°转弯时,应选择图甲中的半径为![]() 的圆弧外车道还是半径为
的圆弧外车道还是半径为![]() 的圆弧内车道?
的圆弧内车道?
(2)做180°转弯时,又应选择图乙中的哪个车道?
请作出必要的计算并据此得出结论。为简化起见,可把赛车作质点处理,且设赛车在刹车减速时四轮同时刹车,并假设赛车在加速过程和减速过程中的加速度的绝对值相等,赛车在直道上高速行驶的速度![]() (空气阻力忽略不计)。
(空气阻力忽略不计)。
【答案】(1)应选择外道行驶
(2)①当![]() ,应选择内道;
,应选择内道;
②![]() ,应选择外道;
,应选择外道;
③当![]() ,选择内、外道均一样
,选择内、外道均一样
【解析】
1.先讨论赛车沿圆弧运动的最大速度,
赛车圆弧运动时所需的向心力由摩擦力提供,与最大静摩擦力相应的运动速度就是允许的最大速度. 如果速度再提高,所需的向心力就大于地面所能提供的摩擦力,因而赛车就不可能沿圆弧运动而将发生侧向滑动,沿圆弧运动的最大速度-与圆半径![]() 、摩擦因数
、摩擦因数![]() 有下列关系:
有下列关系:![]() ,
,
即有![]() . (*)
. (*)
此即赛车沿圆弧运动的最大速度.
2.计算赛车沿直轨道加速行驶或减速行驶的加速度、所用时间及距离.
设赛车在直道上高速行驶时的速度为![]() ,在进入圆弧轨道前要将车速由
,在进入圆弧轨道前要将车速由![]() 降至(*)式中的速度
降至(*)式中的速度![]() . 刹车后,赛车在与地面问的摩擦力作用下减速,赛车的加速度为
. 刹车后,赛车在与地面问的摩擦力作用下减速,赛车的加速度为![]() .
.
赛车自圆弧轨道终点处开始加速. 据题设,其加速度为![]() .
.
赛车由![]() 增至
增至![]() 后,以速度
后,以速度![]() 匀速行驶.
匀速行驶.
根据匀加速运动的公式,加速与减速过程所用的时间![]() 和行驶的距离
和行驶的距离![]() 分别为
分别为
![]() ,
,![]() .
.
3.根据以上分析,我们可以比较沿内道贺沿外道所用时间的长短.
(1)90°转弯时的情况,如图乙所示.
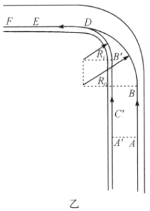
内道和外道的半径分别为![]() 和
和![]() ,沿圆弧轨道的最大速度
,沿圆弧轨道的最大速度![]() 和
和![]() 分别为
分别为![]() ,
,![]() .
.
先讨论赛车沿外道行驶时的情况.
如图乙所示,赛车沿外道行驶时,![]() 为减速过程,由上面的分析可知
为减速过程,由上面的分析可知![]() .
.
![]() 为沿半径为
为沿半径为![]() 的
的![]() 圆周做匀速率
圆周做匀速率![]() 圆周运动,则
圆周运动,则![]() .
.
![]() 为加速过程,时间与
为加速过程,时间与![]() 相同.
相同.
![]() 为匀速(
为匀速(![]() )运动,
)运动,![]() 为赛车沿内道运动加速至速度为
为赛车沿内道运动加速至速度为![]() 时的位置,所以,
时的位置,所以,![]() .
.
因而,赛车在![]() 全过程中所需时间为
全过程中所需时间为
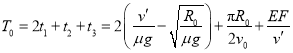
![]() .
.
赛车沿外道行驶时,减速过程和加速过程的距离![]() 和
和![]() 均为
均为![]() .
.
再讨论赛车沿内道行驶时的情况.
如图乙所示,赛车沿内道行驶时,![]() 为匀速(
为匀速(![]() )过程;
)过程;![]() 减速过程,
减速过程,![]() 为沿半径为
为沿半径为![]() 的
的![]() 圆周做匀速率(
圆周做匀速率(![]() )圆周运动;
)圆周运动;![]() 为加速过程;类似于外道的时间计算可得
为加速过程;类似于外道的时间计算可得![]() 所需时间为
所需时间为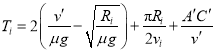
![]() .
.
赛车沿内道行驶时减速过程和加速过程的距离![]() 和
和![]() 均为
均为![]() .
.
由几何关系及![]() 、
、![]() 可得
可得
![]() ,
,![]() .
.
由上述两式及前面的时间关系可得
![]() ,
,![]() .
.
两者之差为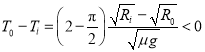 .
.
显然,沿外道所用时间较少,应选择外道行驶.
(2)180°转弯时的情况(图丙)
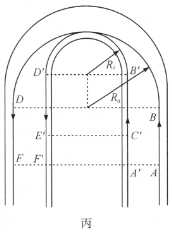
如图丙所示,赛车沿外道行驶时,![]() 为减速过程;
为减速过程;![]() 为匀速率(
为匀速率(![]() )圆周运动;
)圆周运动;![]() 为加速过程;赛车沿内道行驶时,
为加速过程;赛车沿内道行驶时,![]() 为匀速(
为匀速(![]() )过程;
)过程;![]() 减速过程,
减速过程,![]() 为匀速率(
为匀速率(![]() )圆周运动. 根据前面得到的关系可求得:
)圆周运动. 根据前面得到的关系可求得:
赛车沿外道行驶所用时间为![]() .
.
赛车沿内道行驶所用时间为![]() .
.
而![]() ,故
,故![]() ,
,
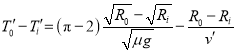
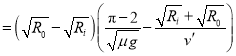 .
.
由上式可得以下结论:
①当![]() ,即
,即![]() 时,
时,![]() ,应选择图丙中的内道;
,应选择图丙中的内道;
②![]() ,即
,即![]() 时,
时,![]() ,应选择图丙中的外道;
,应选择图丙中的外道;
③当![]() ,即
,即![]() 时,
时,![]() ,选择内、外道均一样.
,选择内、外道均一样.

 阅读快车系列答案
阅读快车系列答案