题目内容
【题目】如图所示,三个大小、材质完全相同的小行星,行星(a)上有一个从表面![]() 点到球心
点到球心![]() 的很窄的、试验用的、内壁光滑的矿井;行星(b)上有一个从表面
的很窄的、试验用的、内壁光滑的矿井;行星(b)上有一个从表面![]() 点到球心
点到球心![]() 作为直径的球形空腔;行星(c)因某种原因被运走了半个行星,只剩下一个规则的半球体.
作为直径的球形空腔;行星(c)因某种原因被运走了半个行星,只剩下一个规则的半球体.
(1)在(a)(b)两行星表面![]() 点处无初速地掉入一物体,试计算,在两颗行星中,从
点处无初速地掉入一物体,试计算,在两颗行星中,从![]() 落至球心
落至球心![]() 所用的时间之比以及撞击
所用的时间之比以及撞击![]() 点的速度之比.
点的速度之比.

(2)在行星(c)上,若在原来球形小行星表面的重力加速度为![]() ,问:余下半球圆形表面中心位置的重力加速度
,问:余下半球圆形表面中心位置的重力加速度![]() 为多大?
为多大?
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)我们首先讨论试验井的情况.
设小行星的密度为![]() ,半径为
,半径为![]() ,小物体的质量为
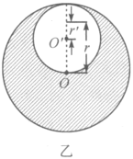
,小物体的质量为![]() .当一个质点处于球体内部时,我们设想球体是由一个个均匀的球壳组成的,由于质量分布均匀的球壳对其内部质点的作用力为零,加之试验井的体积可忽略不计,则不难理解,质点所受的引力为以其所在位置到球心的距离为半径的球体对它的作用力(如图乙所示).所以,小物体在试验井中下落的过程中所受到的引力大小为
.当一个质点处于球体内部时,我们设想球体是由一个个均匀的球壳组成的,由于质量分布均匀的球壳对其内部质点的作用力为零,加之试验井的体积可忽略不计,则不难理解,质点所受的引力为以其所在位置到球心的距离为半径的球体对它的作用力(如图乙所示).所以,小物体在试验井中下落的过程中所受到的引力大小为
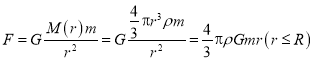 .
.
因此,小物体在试验井中下落的过程中所受到的引力与到小行星中心的距离成正比,并总是指向其球心的.所以,小物体在下落的过程中受到的平均力为
![]() .
.
对小物体的下落过程应用动能定理可得
![]() ,
,
即![]() .
.
由此可得从试验井中落下的小物体撞击球心的速度为
![]() .
.
另一方面,由于小物体在下落过程中的受力满足:![]() ,且总是指向地心的,因此小物体的运动是一简谐运动,从开始下落到地心的时间为
,且总是指向地心的,因此小物体的运动是一简谐运动,从开始下落到地心的时间为![]() 个周期,即
个周期,即
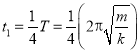 ,
,
式中![]() ,
,
所以,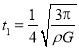 .
.
下面我们来讨论第二个事件发生的情况.此时小行星内部被开采了八分之一,当小物体从入口处落下时,将沿直线撞向球心![]() ,在这一过程中小物体的受力可这样求得,设想将挖走部分重新填充,则小物体在下落的过程中受到的力为整个行星对它的引力与填充部分对它的引力之差,所以,当小物体距球心
,在这一过程中小物体的受力可这样求得,设想将挖走部分重新填充,则小物体在下落的过程中受到的力为整个行星对它的引力与填充部分对它的引力之差,所以,当小物体距球心![]() 为
为![]() 时,距填充球的球心为
时,距填充球的球心为![]() ,则小物体的受力为
,则小物体的受力为
![]() .
.
显然,在这种情况下,小物体在下落过程中所受到的力为恒力,与到球心的距离无关,即小物体在下落过程中做匀加速直线运动,其加速度为
![]() ,则
,则
小物体的撞击速度为![]() .
.
小物体的下落时间为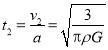 .
.
所以,这两个小物体撞击![]() 点的速度之比为
点的速度之比为
![]() .
.
从![]() 点掉到
点掉到![]() 点的时间之比为
点的时间之比为![]() .
.
(2)先求![]() .
.
由![]() ,即
,即![]() .
.
下面求半球体圆面中心处的![]() .
.
把整个半球体分成![]() 个同心的、等厚的半球壳,每个半球壳的厚度为
个同心的、等厚的半球壳,每个半球壳的厚度为![]() (
(![]() ),对于其中任意一个球壳,讨论其对球心处引力场强的贡献.
),对于其中任意一个球壳,讨论其对球心处引力场强的贡献.
(i)与质量的关系:正比于球壳的质量![]() ,亦即正比于该球壳的半径的平方(
,亦即正比于该球壳的半径的平方(![]() );
);
(ii)与距离的关系:与距离的平方成反比,即![]() .
.
由此可知,球壳对球心处的引力场与球壳的半径无关,则这![]() 个等厚的球壳对球心
个等厚的球壳对球心![]() 点处的引力场强的贡献是相等的.
点处的引力场强的贡献是相等的.
所以,我们只需选出一个球壳作为代表,计算出它对球心![]() 点处的场强的贡献,再乘上
点处的场强的贡献,再乘上![]() ,即得到半球的球心处的引力场强;或者,将所选出的半球的质量乘以
,即得到半球的球心处的引力场强;或者,将所选出的半球的质量乘以![]() ,再计算其对球心
,再计算其对球心![]() 的引力场强的贡献亦可.
的引力场强的贡献亦可.
我们选择最外层的、半径为![]() 的那个半球壳为代表,该球壳的质量为
的那个半球壳为代表,该球壳的质量为![]() ,则整个半球体对球心处的引力场强等效为质量
,则整个半球体对球心处的引力场强等效为质量![]() 、半径为
、半径为![]() 的球壳对其球心处产生的引力场强.
的球壳对其球心处产生的引力场强.
质量为![]() 的球壳对
的球壳对![]() 点处单位质量的质点的作用力等于处于
点处单位质量的质点的作用力等于处于![]() 点的单位质量的质点对半球壳的作用力,而这一作用力的大小通过压强对半球体的作用情况进行类比可知,处在
点的单位质量的质点对半球壳的作用力,而这一作用力的大小通过压强对半球体的作用情况进行类比可知,处在![]() 点处的单位质量的质点对半球体的作用力等于单位质量的质点对半球壳单位面积的作用力乘上
点处的单位质量的质点对半球体的作用力等于单位质量的质点对半球壳单位面积的作用力乘上![]() .
.
所以,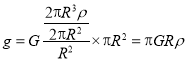 .
.
将![]() 与
与![]() 比较,易得
比较,易得![]() .
.
本题是一道综合程度极高的物理竞赛试题.仅从本题解答过程中涉及的方法来看,我们不难看出,其解答涉及了基本的程序法、平均思想(求平均力![]() )、割补法(在空腔中填充物质)、叠加法(球形空腔内的受力与运动)、微元(半球分割为球壳)、等效(
)、割补法(在空腔中填充物质)、叠加法(球形空腔内的受力与运动)、微元(半球分割为球壳)、等效(![]() 个球均用最外的球壳替代)、建模与假设(在球心
个球均用最外的球壳替代)、建模与假设(在球心![]() 处设置单位质量的物体)、推理(作用力与
处设置单位质量的物体)、推理(作用力与![]() 无关的结论的得出)、类比(将球壳的受力与压强的作用进行比较)等等,将这些方法集中在一道试题中进行应用,没有足够的能力,要顺利地完成解答几乎是不可能的.
无关的结论的得出)、类比(将球壳的受力与压强的作用进行比较)等等,将这些方法集中在一道试题中进行应用,没有足够的能力,要顺利地完成解答几乎是不可能的.
在中学物理竞赛的试题中,类似于上述情况的试题有很多,或同一问题可用多种方法求解,或某一解答可能需用到多种方法.很多情况下,虽然试题的背景、涉及的知识点各有不同,但可能涉及的方法却是一致的.熟练地掌握了处理问题的各种方法,相信同学们处理问题时便会有事半功倍的效果.
但从另一方面讲,本题中每个小间涉及的模型,在我们平时的训练中也都出现过,我们也都能进行相关的处理,而将它们集中在一起,无疑增加了对象与过程,这是增加试题难度的基本形式,而我们的解答过程,实际上是一个拆解过程,将一道综合题拆解成若干个小题,然后再将其“串”接起来,完成问题的解答.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案