Question

【题目】三根质量为、长为的相同均质棒。如图所示地靠在一起，三棒与地接触点的连线成一边长为的正三角形，已知三棒与地之间的摩擦系数相等.

（1）试求棒顶点所受作用力的大小与方向.

（2）若在棒的中点固定一质量也为的小球，再求其顶端所受作用力的大小与方向.

（3）要使体系保持静止，则棒与地面之间的摩擦系数至少为多大？

Answer 1

【答案】（1）（2）（3）

【解析】

（1）三根棒的顶端相互靠在一起，如图甲所示. 由对称性及牛顿第三定律可知，任何一棒（如棒）的顶端受到其余两棒对它的作用力的合力必沿水平方向，如图乙所示.

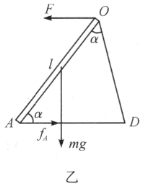
在图甲中是的中点，有，.

由棒所受外力相对点力矩平衡，得，可解得.

（2）当棒的中点固定一质量也为的小球后，三棒的受力情况都发生了改变，且不再对称，但与两棒受力情况相同，此二棒顶端的受力可看成是除原受力外，再各受一个力和的作用，且有. 既然此二棒仍平衡，可见和必沿各自棒的方向，故这两力的合力沿方向，其反作用力作用于棒的顶端，如图丙所示.

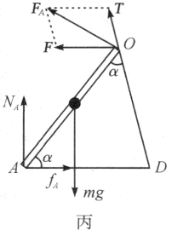
由和小球重力相对点合力矩为零，可得，可解得.

由图丙所示的和的矢量关系，即可求得棒顶端所受的作用力为.

（3）由棒所受的竖直方向和水平方向合外力为零，可分别得

，.

将代入，可解得，.

因为，可得.

棒的受力情况如图丁所示. 由此棒竖直方向和水平方向合外力为零，可分别得

，.

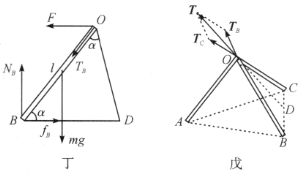
由图戊所示的矢量关系，可得、与的关系为，

即.

由此而得，.

再由，可得.

由于、棒受力情况完全相同，故棒平衡所需的最小摩擦系数与棒相等. 比较与的大小，即可的棒与地面的摩擦系数应满足.

本题是有关空间力系的经典试题，涉及空间几何关系的运算、对称分析、一般物体的平衡研究、临界状态的分析、不确定关系的判断等等.

对于第（3）问的求解，除了对空间问题的认识可能出现错误外，很容易遗漏对或棒平衡所需最小摩擦系数的讨论和求解，误以为小球是固定在棒的中点，只要棒能保持平衡，则体系一定能平衡，从而得到只需满足的错误结论.