题目内容
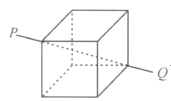
【题目】如图所示，匀质立方体的边长为
，质量为
.试求该立方体绕对角线轴
的转动惯量
.
【答案】
【解析】
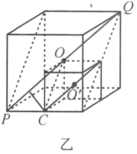
如图乙所示，将立方体分为边长为
的八个小立方体，则由几何关系可知，其中有6个小立方体的对角线到大立方体的对角线的距离为
.
设大立方体绕对角线转动的转动惯量为
，则小立方体绕对角线转动的转动惯量为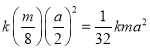
，显然，这里的
是一个无量纲的常量.
取匀质立方体对角顶点在转轴上，由平行轴定理可得
.
将
代入可得
，
所以，.
本题的解答显然也注意到了对称性及叠加原理的应用，更重要的是本题对立方体转动惯量的假设，即大立方体绕对角线转动的转动惯量为，这体现了答题者对转动惯量本质的认识，也是量纲法在此种情况下的应用.
本题难度虽然不大，但其综合程度并不低，同学们在学习过程中，应充分注意到此类习题的练习功能，以提高自己综合运用知识的能力.
练习册系列答案
相关题目
