题目内容
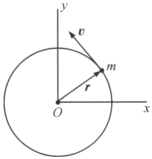
【题目】如图甲所示,S为离子源,它能各向同性地发射质量为m、电量为q、速率同为![]() 的离子。S右侧有一半径为R的圆屏,S与圆屏中心O的连线垂直于圆屏。设周围空间有匀强磁场,磁感应强度B的方向与S到O的方向一致。S发射的离子中,有些离子不管S、O之间的距离如何变化,总能打到屏面上,试求这些离子的数目占总发射离子数的百分比。解题时不必考虑离子间的相互作用。
的离子。S右侧有一半径为R的圆屏,S与圆屏中心O的连线垂直于圆屏。设周围空间有匀强磁场,磁感应强度B的方向与S到O的方向一致。S发射的离子中,有些离子不管S、O之间的距离如何变化,总能打到屏面上,试求这些离子的数目占总发射离子数的百分比。解题时不必考虑离子间的相互作用。

【答案】![]()
【解析】
将从S射出的离子初速度![]() 与B的夹角记为
与B的夹角记为![]() ,那么
,那么![]() 与B垂直的分量为
与B垂直的分量为![]() 。
。
离子在匀强磁场中将作等距螺旋线运动,旋转的圆半径为:![]() 。
。
对于不管S、O之间的距离如何变化总能打到屏上的离子,要求满足
![]() ,即
,即![]() 。
。
取![]() 的下限
的下限![]() 满足:
满足:![]() 。
。
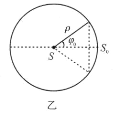
以S为球心,某个长度参量![]() 为半径作一球面,在此球面上取一球帽,使其与
为半径作一球面,在此球面上取一球帽,使其与![]() 有如图乙所示的对应关系,那么,从S发出的离子凡是能打在此球帽上的,均为符合要求的粒子,考虑到粒子是各向同性发射的,符合要求的离子数目占总离子数目的百分比k,即为球帽面积
有如图乙所示的对应关系,那么,从S发出的离子凡是能打在此球帽上的,均为符合要求的粒子,考虑到粒子是各向同性发射的,符合要求的离子数目占总离子数目的百分比k,即为球帽面积![]() 与球面面积
与球面面积![]() 之比,根据数学中给出的球帽公式,有
之比,根据数学中给出的球帽公式,有
![]() 。
。
于是,所求k值便为
![]() 。
。
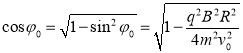 ,
,
代入得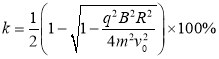 。
。
讨论:
上述结论仅对![]() 时成立。
时成立。
若![]() ,则因
,则因![]() ,
,
对任意![]() 都有
都有![]() ,因此向右发射的离子均能打到屏上,即恒有
,因此向右发射的离子均能打到屏上,即恒有![]() 。
。

练习册系列答案
相关题目