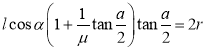题目内容
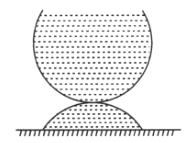
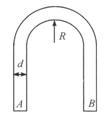
【题目】有一半径为![]() 的圆柱
的圆柱![]() ,静止在水平地面上,并与竖直墙面相接触。现有另一质量与
,静止在水平地面上,并与竖直墙面相接触。现有另一质量与![]() 相同,半径为
相同,半径为![]() 的较细圆柱
的较细圆柱![]() ,用手扶着圆柱
,用手扶着圆柱![]() ,将
,将![]() 放在
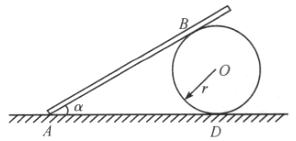
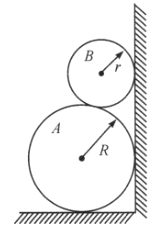
放在![]() 的上面,并使之与墙面相接触,如图所示,然后放手。已知圆柱
的上面,并使之与墙面相接触,如图所示,然后放手。已知圆柱![]() 与地面的静摩擦系数为0.20,两圆柱之间的静摩擦系数为0.30,,若放手后,两圆柱体能保持如图所示的平衡,问:圆柱
与地面的静摩擦系数为0.20,两圆柱之间的静摩擦系数为0.30,,若放手后,两圆柱体能保持如图所示的平衡,问:圆柱![]() 与墙面间的静摩擦系数和圆柱的
与墙面间的静摩擦系数和圆柱的![]() 半径
半径![]() 的值各应满足什么条件?
的值各应满足什么条件?
【答案】![]()
【解析】
放上圆柱![]() 后,圆柱
后,圆柱![]() 有向下运动的倾向,对圆柱
有向下运动的倾向,对圆柱![]() 和墙面有压力.圆柱
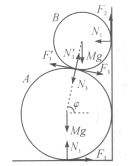
和墙面有压力.圆柱![]() 倾向于向左运动,对墙面没有压力.平衡是靠各接触点的摩擦力维持的.现设系统处于平衡状态,取圆柱
倾向于向左运动,对墙面没有压力.平衡是靠各接触点的摩擦力维持的.现设系统处于平衡状态,取圆柱![]() 受地面的正压力为
受地面的正压力为![]() ,水平摩擦力为
,水平摩擦力为![]() ;圆柱
;圆柱![]() 受墙面的正压力为
受墙面的正压力为![]() ,竖直摩擦力为
,竖直摩擦力为![]() ,圆柱
,圆柱![]() 受圆柱
受圆柱![]() 的正压力为
的正压力为![]() ,切向摩擦力为
,切向摩擦力为![]() ;圆柱
;圆柱![]() 受圆柱
受圆柱![]() 的正压力为
的正压力为![]() ,切向摩擦力为
,切向摩擦力为![]() ,如图所示.各力以图示方向为正方向.
,如图所示.各力以图示方向为正方向.
已知圆柱![]() 与地面的摩擦系数
与地面的摩擦系数![]() ,两圆柱间的摩擦系数
,两圆柱间的摩擦系数![]() .设圆柱
.设圆柱![]() 与墙面的摩擦系数为
与墙面的摩擦系数为![]() ,过两圆柱中轴的平面与地面的交角为
,过两圆柱中轴的平面与地面的交角为![]() 。
。
设两圆柱的质量均为![]() ,为了求出
,为了求出![]() 以及为保持平衡所需的
以及为保持平衡所需的![]() 之值,下面列出两圆柱所受力和力矩的平衡方程。
之值,下面列出两圆柱所受力和力矩的平衡方程。
对圆柱![]() ,有
,有
![]() , ①
, ①
![]() , ②
, ②
![]() . ③
. ③
对圆柱![]() ,有
,有
![]() , ④
, ④
![]() , ⑤
, ⑤
![]() . ⑥
. ⑥
由于![]() ,得
,得
![]() , ⑦
, ⑦
式中![]() 代表
代表![]() 和
和![]() 的大小。又因
的大小。又因![]() ,于是式①②④⑤四式成为
,于是式①②④⑤四式成为
![]() , ⑧
, ⑧
![]() , ⑨
, ⑨
![]() , ⑩
, ⑩
![]() .
.
以上四式是![]() 和
和![]() 的联立方程,解这联立方程可得
的联立方程,解这联立方程可得
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
式是平衡时所需要的力,![]() 没有问题,但
没有问题,但![]() 三个力能不能达到所需要的数值
三个力能不能达到所需要的数值![]() ,即式要受摩擦系数的制约.三个力中只要有一个不能达到所需的
,即式要受摩擦系数的制约.三个力中只要有一个不能达到所需的![]() 值,在那一点就要发生滑动而不能保持平衡。
值,在那一点就要发生滑动而不能保持平衡。
首先讨论圆柱![]() 与墙面的接触点.接触点不发生滑动,要求
与墙面的接触点.接触点不发生滑动,要求
![]() 。
。
由式得,![]() ,
,
所以,![]() .
.
再讨论圆柱![]() 与地面的接触点的情形.按题设,此处的摩擦系数为
与地面的接触点的情形.按题设,此处的摩擦系数为![]() ,根据摩擦定律
,根据摩擦定律![]() ,若上面求得的接触点维持平衡所需的水平力
,若上面求得的接触点维持平衡所需的水平力![]() 满足
满足![]() ,则圆柱在地面上不滑动;若
,则圆柱在地面上不滑动;若![]() ,这一点将要发生滑动。
,这一点将要发生滑动。
圆柱![]() 在地面上不发生滑动的条件是
在地面上不发生滑动的条件是
![]() .
.
由图乙可知![]() ,
,
则![]() .
.
由式以及![]() ,可以求得
,可以求得
![]() .
.
即只有当![]() 时,圆柱A在地面上才能不滑动。
时,圆柱A在地面上才能不滑动。
最后讨论两圆柱的接触点.
![]() .
.
由式以及![]() ,可解得
,可解得
![]() .
.
显然,在平衡时,![]() 的上限为
的上限为![]() .总结式和式,得到
.总结式和式,得到![]() 满足的条件为
满足的条件为
![]() .
.