题目内容
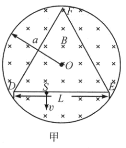
【题目】如图所示，屋架由同一竖直面内的多根无重杆绞接而成，各绞接点依次为1，2，…，9，其中，绞接点8、2、5、7、9位于同一水平直线上，且9可以无摩擦地水平滑动。各绞接点间沿水平方向上的间距和沿竖直方向上的间距如图所示，绞接点3承受由竖直向下的压力
，点1承受有竖直向下的压力
，求铰接点3和4间杆的内力.
【答案】
【解析】
如图甲所示,屋架由同一竖直面内的多根无重杆铰接而成,各铰接点依次为
,其中,铰接点
位于同一水平直线上,且9可以无摩擦地水平滑动.各铰接点间沿水平方向上的间距和沿竖直方向上的间距如图甲所示,铰接点3承受有竖直向下的压力
,点1承受有竖直向下的压力,求铰接点3和4间杆的内力。
方法1：由于点9可沿水平方向无摩擦滑动,故屋架在点9处所受外力只可能沿竖直方向,设为
.由于屋架所受外力、和均沿竖直方向,则屋架在点8所受的外力也只可能沿竖直方向,设其为
。
以整个屋架为对象,列出各外力对支点8的力矩平衡方程,有
,
所以,
,
的方向竖直向上。
又由整个屋架的受力平衡关系,应有
，
所以,
，
的方向竖直向上。
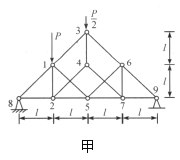
假设将铰接点5、6、7、9这部分从整个屋架中隔离出来,则这部分受到杆15、杆47、杆36的作用,这几个作用力均沿与杆15平行的方向,设其以一个力
表示,则这个力也必与杆15方向平行,此外,这部分还受到杆25的作用,设其为
,显然的方向应沿水平方向;这部分还受到支持力的作用.这样,这部分就等效为受、和三个力的作用而平衡.由此表示此三力的矢量构成一个封闭三角形,由前述此三力的方向关系可以确定,这一三角形只能是如图乙所示的三角形。
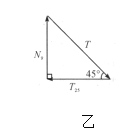
由此三角形可见
.
杆25对点5的作用力方向水平向左,可见杆25中的内力为张力。
又假设取铰接点8为研究对象,它受到支持力和杆82对它的作用力
和杆81对它的作用力
,由于此三力平衡,则与的合力必沿杆81的方向，可见应有
且的方向应水平向右,即杆82的内力为张力
再假设取铰接点2为研究对象，由以上分析知,其左、右两水平杆对它的作用力均为拉力,其大小分别为和,而另外只有杆24能对点2提供水平方向的分力,则为使点2在水平方向受力平衡,杆24作用于点2的力必沿由2指向点4的方向,进而为使点2在竖直方向上受力平衡,则杆12对点2的作用力必沿竖直向下的方向。
综合上述,可得点2的受力如图丙所示。
由图知
,
故得
.
即杆24中的内力为张力,其大小为
.
最后以点4为研究对象,它受到与之相连的三根杆的三个力的作用.此三力应互相平衡.现以
表示这三个力,由于
的方向是确定的(杆42的内力为张力,则必沿由点4指向点2的方向),而
又只能沿对应杆的方向,则此三力只可能取如图丁所示的方向.由点4在水平方向的受力平衡,应有
，
所以,
.
由点4在竖直方向的平衡,应有
.
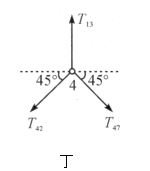
即杆43中的内力为张力,大小为.
