题目内容
【题目】如图所示,![]() 轴右边存在磁感应强度为
轴右边存在磁感应强度为![]() 的匀强磁场,
的匀强磁场,![]() 轴左边存在磁感应强度为
轴左边存在磁感应强度为![]() 的匀强磁场,它们的方同皆垂直纸面向里.在原点
的匀强磁场,它们的方同皆垂直纸面向里.在原点![]() 处,一个带正电的电荷量为
处,一个带正电的电荷量为![]() 、质量为
、质量为![]() 的粒子
的粒子![]() ,在
,在![]() 时以大小为
时以大小为![]() 的初速度沿正
的初速度沿正![]() 轴方向运动,在粒子
轴方向运动,在粒子![]() 开始运动后,另一质量和电荷量都与
开始运动后,另一质量和电荷量都与![]() 相同的粒子
相同的粒子![]() ,从原点
,从原点![]() 以大小为
以大小为![]() 的初速度沿负
的初速度沿负![]() 轴方向开始运动.要想使
轴方向开始运动.要想使![]() 和
和![]() 能在运动过程中相遇,试分析和计算它们出发的时间差的最小值,并求出与此对应的相遇地点的坐标.设整个磁场区域都处于真空中,且不考虑重力及
能在运动过程中相遇,试分析和计算它们出发的时间差的最小值,并求出与此对应的相遇地点的坐标.设整个磁场区域都处于真空中,且不考虑重力及![]() 、
、![]() 两粒子之间的相互作用力.
两粒子之间的相互作用力.

【答案】![]() ;
;![]() ,
,![]()
【解析】
带电荷量为![]() 、质量为
、质量为![]() 、初速度为
、初速度为![]() 的粒子,当它在磁感应强度为
的粒子,当它在磁感应强度为![]() 的匀强磁场中运动时,如果其初速度的方向与磁场方向垂直,由洛仑兹力和牛顿定律可知,它将在磁场中做匀速圆周运动.令
的匀强磁场中运动时,如果其初速度的方向与磁场方向垂直,由洛仑兹力和牛顿定律可知,它将在磁场中做匀速圆周运动.令![]() 和
和![]() 分别表示其周期和轨道半径,则有
分别表示其周期和轨道半径,则有
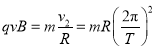 . ①
. ①
由此求得 ![]() , ②
, ②
![]() . ③
. ③
把这些结论用到本题中,可知![]() 粒子开始在第一象限中运动(
粒子开始在第一象限中运动(![]() 轴以右),有
轴以右),有
![]() , ④
, ④
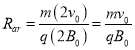 . ⑤
. ⑤
经半个周期(即![]() )后,进入第二、三象限中(
)后,进入第二、三象限中(![]() 轴以左),周期和轨道半径变为
轴以左),周期和轨道半径变为
![]() , ⑥
, ⑥
![]() . ⑦
. ⑦
以后就按此模式在![]() 平面内沿图乙中的虚线运动.
平面内沿图乙中的虚线运动.
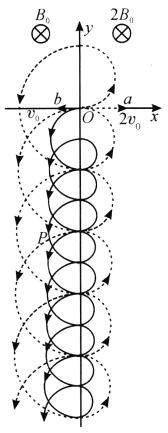
同理,粒子![]() 开始在第三象限(
开始在第三象限(![]() 轴以左)中运动,有
轴以左)中运动,有
![]() , ⑧
, ⑧
经半个周期(即![]() )后,进入第四象限(
)后,进入第四象限(![]() 轴以右)运动,周期和轨道半径变为
轴以右)运动,周期和轨道半径变为
![]() , ⑩
, ⑩
![]() .
.
以后就按此模式在![]() 平面内沿图中实线运动.由以上分析可知,只要在右边,不管是
平面内沿图中实线运动.由以上分析可知,只要在右边,不管是![]() 还是
还是![]() ,周期皆为
,周期皆为![]() ;只要在左边,周期皆为
;只要在左边,周期皆为![]() .
.
由图乙可见,只有在两轨迹交叉或相切的那些点,才有相遇的可能性.为求得题中所说的时间差的最小值,下面我们先假设,如果![]() 、
、![]() 同时开始运动,分析经过哪个交叉或相切点时两者的时间差最短,则这个时间差就应当等于题中所说的要
同时开始运动,分析经过哪个交叉或相切点时两者的时间差最短,则这个时间差就应当等于题中所说的要![]() 、
、![]() 在此交叉或相切点能相遇时,两者出发时间的时间差.为此,结合图乙分别考查
在此交叉或相切点能相遇时,两者出发时间的时间差.为此,结合图乙分别考查![]() 、
、![]() 的运动,经过分析就可看出,在
的运动,经过分析就可看出,在![]() 到
到![]() 之间的那个交叉点(图乙中的
之间的那个交叉点(图乙中的![]() 点)处,
点)处,![]() 、
、![]() 通过它的时间差最短(在
通过它的时间差最短(在![]() 以前和
以前和![]() 以后的那些交叉或相切点,
以后的那些交叉或相切点,![]() 、
、![]() 通过时的时间差都较长).
通过时的时间差都较长).
为了定量地求出此时间差,取负![]() 轴上距原点
轴上距原点![]() 为
为![]() (即
(即![]() )处为新的原点
)处为新的原点![]() ,如图所示.取时间
,如图所示.取时间![]() 为新的起始计时时刻,对
为新的起始计时时刻,对![]() 用
用![]() 表示,对
表示,对![]() 用
用![]() 表示.在
表示.在![]() 轴以左
轴以左![]() 、
、![]() 的周期相同,所以角速度亦相同,以
的周期相同,所以角速度亦相同,以![]() 表示
表示![]() 、
、![]() 在
在![]() 轴以左的角速度,有
轴以左的角速度,有
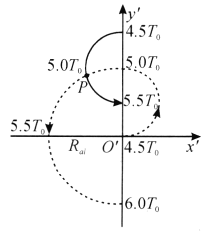
![]() .
.
对![]() ,有
,有
![]() ,
,
![]() .
.
对![]() ,有
,有
![]() ,
,
![]() .
.
对![]() 点应有
点应有
![]() ,
,![]() .
.
由以上各式可解得所求的时间差应为
![]() .
.
这个结果说明,如![]() 、
、![]() 同时出发,则
同时出发,则![]() 比
比![]() 晚
晚![]() 时间通过
时间通过![]() 点.换成题目的要求,就应当说,要
点.换成题目的要求,就应当说,要![]() 、
、![]() 相遇,则
相遇,则![]() 的出发时间应比
的出发时间应比![]() 晚
晚![]() .
.
由以上各式还可求得![]() 点的坐标为
点的坐标为
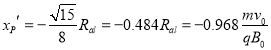 ,
,
![]() .
.
换为![]() 坐标系,有
坐标系,有
![]() ,
, ![]()
![]() .
. ![]()
类似于本题中的粒子在![]() 轴方向的“漂移”运动,是研究带电粒子在电场或磁场中运动时经常讨论的问题之一.讨论这一问题必然会涉及带电粒子在运动过程中在时间与空间问题上的周期性讨论,有时候这类问题看上去只是几何关系的寻找,有点类似于行程与相遇问题而被我们轻视,但这一关系却往往会成为我们解答问题的瓶颈.
轴方向的“漂移”运动,是研究带电粒子在电场或磁场中运动时经常讨论的问题之一.讨论这一问题必然会涉及带电粒子在运动过程中在时间与空间问题上的周期性讨论,有时候这类问题看上去只是几何关系的寻找,有点类似于行程与相遇问题而被我们轻视,但这一关系却往往会成为我们解答问题的瓶颈.
处理这类问题,我们虽然有“跟着过程走”的口诀,但在具体的执行过程中,我们有时很难坚持做到.平时训练时,对这类试题一定不要觉得 “简单”而厌烦其过程分析,避免在考试时出现在心理上回避此类问题的情况.








