题目内容
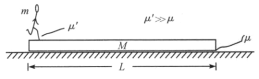
【题目】有一装置如图所示，巳知滑动A的重力为
，滑块B的重力为2G，分别放在光滑斜面上，左、右两个斜面的倾角分别为60°和30°。两滑块和球C、D用轻绳连接，C、D各重
。
（1）平衡时的
和
角多大？
（2）现将连接C、D的绳剪断，求剪断后的瞬间滑块A、B的加速度。
【答案】（1）
（2）
，
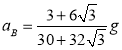
【解析】
（1）平衡的时候，对
物体有
.
对
物体有
.
对
、
两物体有
.
同时：
，可解得
.
（2）在、之间的绳刚被剪断的瞬间，设的加速度的水平分量为
（向右），竖直分量为
（向上）. 根据牛顿第二运动定律，有
对：
.
对：
.
对：
，
.
由以上四式可解得
，
.
第（1）问是静平衡问题，这种情况，多数是为第（2）问做铺垫，赋予第（2）相应的条件.
剪断、间的连线后，呈现给我们的是一个多体的动力学问题，从解答中我们不难看出，其连接体间的加速度关联显然是我们突破障碍的要点.
说明的是，此处的加速度关联仅仅只适用于绳子尚未运动起来的情况，一旦绳子运动起来，亦即绳子转动起来了，这种关联便不再成立了.
练习册系列答案
相关题目
