题目内容
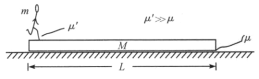
【题目】如图所示，设初始时，人和板均静止，从某一时刻起，人在板上加速运动，到达板右端，骤然停止，此后人和板一起向右滑动，求滑动的最大距离l。（相关数据如图所示）
【答案】
【解析】
这里所求的人、板向右滑动的最大距离，是指人在板上的各种运动方式中，可以使人、板向右滑动最大距离所对应的某一种运动方式. 这对应着人在板上做加速运动时板
动与不动的两种情况.
若不动，当人到达板的右端骤然停止时，人的动量即为系统的动量，它决定了系统后面运动的初速度.
由
可知，人在加速阶段，
越大，
越大. 所以，对于地面的滑动距离而言，人在板上的加速度越大越好. 此种情况下的最大加速度为
，当人的加速度大于这一值时，板将发生滑动.
若人在加速阶段，在向左滑动，此时选择人、板组成的系统进行讨论：这种情况下，人与板间的作用力为内力，它不改变系统的动量，能改变系统动量的只是外力，即地面对的摩擦力（方向向右），而摩擦力的大小是定值，即
.
为了使系统得到最大的动量，就应增加作用时间，这就意味着要减小人的加速度，而这种情况下，人的最小加速度也为，因为人只有大于这一加速度，板才有可能运动.
综上所述，选择将动而未动时的情况为最佳，即人的加速度为.
在人的加速与板的滑动两种情况下，外力大小均为
，动量的变化值也相等，因而作用时间也相等，则
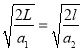，其中
，
.
由此易得.
本题亦是一个多对象（人和板）、多过程（人在板上运动与人、板一起向前滑动）问题，同时还涉及多状态（人在板上跑动时，极滑动与不滑动两种情况），特别是多状态是隐性的，如果没有对题干中“各种运动方式”作出正确的理解与分析，必然对整个模型与整个过程感到迷茫，有一种无从下手的感觉.
正确地理解题意，全面构建出符合题意的模型，冷静比较，分析状态变化的临界态，合理筛选出极值态，才能找到通达结果的合理路径，而完成这一系列操作是需要很强的综合能力的.
