题目内容
【题目】图所示,在![]() 的空间区域内(y,z方向无限延伸)均匀分布着密度为
的空间区域内(y,z方向无限延伸)均匀分布着密度为![]() 正电荷,此外均为真空.
正电荷,此外均为真空.
(1)试求![]() 处的场强分布。
处的场强分布。
(2)若将一质量为m,电量为![]() 的带电质点,从
的带电质点,从![]() 处由静止释放,试问:该带电质点经过多长时间第一次到达
处由静止释放,试问:该带电质点经过多长时间第一次到达![]() 处?
处?

【答案】(1)![]()
![]() 时,场强与x轴同向;
时,场强与x轴同向;![]() 时,场强与x轴反向.(2)
时,场强与x轴反向.(2)
【解析】
给定区域电荷分布均匀且对称,在y、z向无限伸展的特点,我们想象存在这样一个圆柱体,底面积为S,高为2x,左、右底面在x轴上的坐标分别是![]() 和x,如图所示。可以判断圆柱体左、右底面处的场强必定相等,且方向分别是逆x轴方向和顺x轴方向.再根据高斯定理,便可求出坐标为x处的电场强度。
和x,如图所示。可以判断圆柱体左、右底面处的场强必定相等,且方向分别是逆x轴方向和顺x轴方向.再根据高斯定理,便可求出坐标为x处的电场强度。
(1)根据高斯定律,有
![]()
坐标为x处的场强为
![]()
![]() 时,场强与x轴同向;
时,场强与x轴同向;![]() 时,场强与x轴反向.
时,场强与x轴反向.
(2)若将一质量为m、电量为![]() 的带电质点置于此电场中,质点所受的电场力为
的带电质点置于此电场中,质点所受的电场力为
![]() .
.
显然质点所受的电场力总是与位移x成正比,且与位移方向相反,符合准弹性力的特点.质点在电场力的运动是简谐振动,振动的周期为
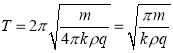
当质点从![]() 处静止释放,第一次达到
处静止释放,第一次达到![]() 处所用的时间为
处所用的时间为
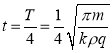 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目