Question

【题目】形状如同通常铅笔的正六角棱柱，质量为M，密度均匀，其横截面六边形边长为。

试求：

（1）该棱柱体相对于它的中心对称轴的转动惯量。

（2）该棱柱体相对于它的某一棱的转动惯量。

Answer 1

【答案】(1) (2)

【解析】

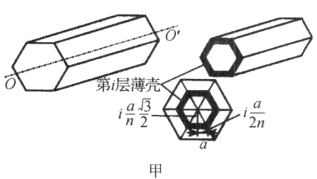
（1）这里求的是规则形状的几何体关于它的中心对称轴的转动惯量。从转动惯量的定义出发，我们可将棱柱沿截面的径向均匀分割成个厚度均为、棱长为l的六棱柱薄壳，如图甲甲所示，确定任意一个这样的薄壳对中心轴的元转动惯量，然后求和即可，即。

现在，先给出一矩形薄板关于与板的一条边平行的轴的转动惯量。板的尺寸标注如图乙所示，质量为m，且均匀分布，轴与板的距离为h，沿b边将板无限切分成n条长、宽的窄条，则有

.

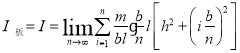
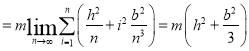回到先前的六棱柱薄壳元上，由对称性可知，薄壳元对轴的转动惯量是，即

，

式中是六棱柱的密度，大小为

.

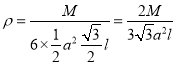则六棱柱体对中心对称轴的转动惯量

.

（2）.利用平行轴定理，我们可求得六棱柱相对于棱边的转动惯量为