题目内容
【题目】如图所示，一个半径为R，水平放置的光滑圆形轨道上，有两个可自由运动的小球，其质量分别为m和M。现有一个质量可忽略的弹簧，将两小球分别顶在弹簧两端，用细线将小球压紧弹簧后捆邦在一起。
（1）如果细线断了，弹簧将两小球沿相反方向弹射出去，而弹簧离开轨道，两小球将在轨道何处发生碰撞？（如图所示，用
知表示）。
（2）设弹簧被压缩时具有的热能为
，求从断线到发生碰撞的时间间隔
。
（3）若碰撞是完全弹性的正碰撞，问：两球在第一次发生碰撞后，又在何处发生第二次碰撞？
【答案】（1）
（2）
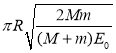（3）第二次碰撞发生处仍然是断线处
【解析】
（1）设断线的瞬间，水平方向不受力，动量守恒，则
，即。
设碰撞发生前M，m分别经过角度
、
，则
。
又由图可知，
，
所以
，得。
（2）从断线到碰撞发生，由能量守恒，有
。
又，代人得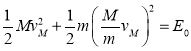
，
解得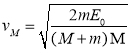
。
则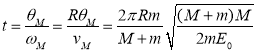
。
（3）因为第一次碰撞时有
，
其中：
，
为碰前各自的速度；
，
为碰后两者的分离速度，可见
。
又由能量守恒有
，
所以第二次碰撞发生处仍然是断线处。
练习册系列答案
阳光课堂课时作业系列答案
相关题目
