Question

【题目】在一个大湖的岸边（可视湖岸为直线）A处停放着一只小船，缆绳突然断开，小船被风刮跑，以的速度匀速向湖中行驶，其方向与湖岸成角。另有一人在缆绳断开时从A点出发，他先沿湖岸走一段后再入水游泳去追船。已知人在岸上走的速度，在水中游泳的速度为。问：此人能否追上小船？若能，小船被人追上的最大速度为多少？

Answer 1

【答案】可见小船被人追上时的最大速度为，故人能追上小船。

【解析】

解析1：由于人在水中的游速小于小船在水中的速度，因此，人只有先沿岸跑一段路程后再入水游泳追船，这样才有可能追上小船。设法求出小船被人追上的最大速度，即可知人能否追上小船。

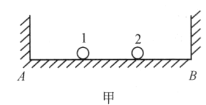
设船速为v，人追上小船的时间为t，设人在岸上跑的时间是整个追赶时间的k倍，人要追上船，则船运动的路线与人运动的两段路线构成一个三角形，如图甲所示，由余弦定理得

，

整理得。

要使上列方程在范围内有解，则需，故有

，

所以，

配方整理得，

两边开方，解得。

可见小船被人追上时的最大速度为，故人能追上小船。

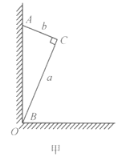
解析2：用作图法可以求出在追上小船的时间t内，人在岸上跑和在水中游所能达到的区域。若在此时间内，船没有跑出该区域，就证明船能被人追上，由船与该区域边界的交点，可以求出船能被人追上的最大速度。

如图乙所示，设人从A点起在时间t内沿湖岸跑过路程达到B点，。若人从A点起，在水中游时间t，则可以到达的区域是以A为圆心，为半径的半圆，若人先在岸上跑时间到C点，然后再在水中游时间，则，在时间内人可以到达以C为圆心、为半径的半圆区域。同理，选取不同的，可以得到不同的入水点C，以C为圆心、为半径可以作出无数个半圆。由数学的包络线可知，这些半圆之公切线为BE和OD。因此，在追赶时间t内，人所能达到的区域边界为湖岸AB和切线OD、BE以及圆弧DE。由于船的速度矢量与边界BE相交于点M，则当时，船能被人追上，可见，要在M点追上船，必须在岸边选择一个合适的入水点。

因为，

为直角三角形，所以

，

解得。

又因为，

所以，而，

所以，

故为等腰直角三角形。

由得，

则。

可见小船被人追上时的最大速度为，故人能追上小船。