Question

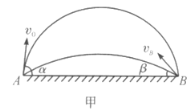
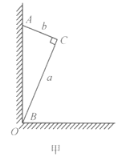
【题目】（1）如图甲所示，直角三角板的AB边紧靠墙壁，已知，，且，现今A点沿墙壁向O点运动，B点沿地面远离O点运动，直至AB与地面重合，求C点经过的路程。

（2）现将三角板换成量角器，量角器半径为R，开始时量角器的直径紧贴竖直墙壁，其运动方式与三角板的运动方式类同，最后它的直径与水平面相贴，求量角器倒下时扫过的面积。

Answer 1

【答案】（1）（2）

【解析】

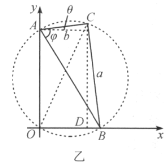
解析1．作出任意时刻三角板所处的位置如图乙所示，并将其置于坐标系中，其中x轴水平向右，y轴竖直向上，O点为墙角。设该时刻AC边与水平线的夹角为，，连接OC。

因为，，由此可以推出四边形AOBC有外切圆。

因同一个圆的同一段弧所对的圆周角必相等，故，很显然，三角板的一个角是定值，得是一定值，这表明C仅在与地面夹角为的直线上运动，相对于某一瞬时的可求出，

。

因，，

其中是从到0再到的一个连续变化，所以

，

。

因此

。

2．由1的讨论，易知C点离O点最远的情形，即该直角三角形ABC，在整个过程中C点所能达到的最远处为，显然。因此，对直径为2R的量角两器应有。如图丙所示。所以量角器边缘上各点能达到的最远的地方都是在离O点2R的地方。因此，量角器倒下时扫过的面积为

。