题目内容
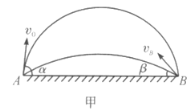
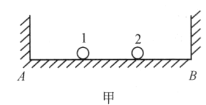
【题目】如图甲所示，有两个等质量的小球，在一光滑的水平直滑槽AB内运动，滑槽两端有固定的壁。两球之间及小球与壁之间的碰撞都是完全弹性的（即两球经过碰撞交换速度）．开始时，1、2两球分别位于将滑槽三等分的两个分点处，两球不等速但同方向。
(1)．若两球之间的第二次碰撞是在滑槽中点迎面相碰，求两球初速的比值；
(2)．若两球之间的第5次碰撞是在滑槽中点迎面相撞，求两球初速的比值，并回答满足要求的解有几种。
提示：可以先求出满足要求的一种解（即初速比值），再求出满足要求的所有的可能解。
【答案】（1）
（2）
，
时，
； ，
时，
： ，
时，
； 
，时，
； 
，时，
。
【解析】
由于小球可视为质点且质量相同，碰撞又是完全弹性的，所以两球每次碰撞之后，相互“交换速度”。因此，可以把两个小球的运动过程等效为两个彼此互不相碰的小球各自独立按自己的初速在两墙壁间运动。下面所说的两小球就是指这样的两个等效的小球。
对这种情况，可使用图乙所示的
图来说明两小球在各时刻的位置。A、B为导轨的两端，设小球1的初速为
，其在导轨中的单独运动如图中的实线所示，小球2的初速为
，其单独运动如图中虚线所示（设
）。实线与虚线的每个交点都代表一次碰撞。
1．如图丙所示，设AB长为l，则到第2次碰撞（为迎面相碰）时，小球1、2走过的路程分别为
，
，
可得。
2．一种解可参看图丙所示求得。此时
，
，
所以。
下面考虑满足要求的所有可能解，设在t时刻两小球在滑槽中点相碰，则小球1、2所经过的路程分别为
，
。
式中n与k可为零或任何正整教。由上述两式得到
。
按本题要求，两球在滑槽中点相碰前必须经过4次碰撞，两球在中点的碰撞为迎面相碰，则两球中必须至少有一小球路程大于
，小于
，因而n、k中必须至少有一个为4，另一个的取值则可为0、1、2、3、4。又当n为奇数时，小球1在t时刻的运动方向为由B向A，n为偶数时为由A向B；k为奇数时，小球2在t时刻的运动方向为由A向B，k为偶数时为由B向A。若要两球在t时刻迎面相碰，必须
为偶数。故
取值只能是
，
，
，
，
5种。代入上式得
，时，；
，时，：
，时，；
，时，；
，时，。
共5种解。
