题目内容
【题目】如图所求，半径为
的空心球绕其本身竖直轴线旋转，角速度
，在球内高度为
处有一木块随同球一起旋转。问：
（1）摩擦因数至少为多少时才能实现这一情况？
（2）当
时，实现这一情况的条件是什么？
（3）如果木块的位置有微小的变化或球的角速度有微小的变化，木块的稳定性如何？
【答案】（1）0.2259 （2）0.1792 （3）略
【解析】
木块在运动过程中受到球面静摩擦力的作用，要注意静摩擦力的方向，第（3）问讨论木块的稳定性的方法比较有一般性.
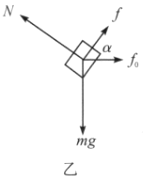
因为要求的是最小摩擦因数，所以可以考虑是最大静摩擦力．静摩擦力的方向尚不明确，我们可以先让它沿切线方向向上（即木块有向下的滑动趋势）. 此时木块在转动参照系中受到四个力而平衡：重力
、摩擦力
，弹力
、惯性力
（如图乙所示）.
由平衡条件有
，
.
可解得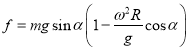
，
.
（1）将
的数据代入，
，可见是沿切线方向向上的，因此
.
（2）将
的数据代入，
，可见是沿切线方向向下的，因此
.
（3）要研究当木块位置有微小变动（即
有微小变动）或角速度
有微小变动时木块的稳定性，必须要看
与、的相关性. 但从（1）（2）中的表达式可看出与、的关系是比较复杂的，此时我们可以用作图像的方法来看它们的相关性.
和、粗略的图像如图丙所示.
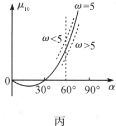
从图中可看出：如果不变而木块上滑（即变大），那么变大，即需要较大的静摩擦因数才能稳定，现在的
不够大，因此木块将滑回原处；如果不变而变小，那么变小，即只需较小的静摩擦因数就能稳定，现在的已足够，所以木块不会回到原处. 如果不变而变大，那么变小，所需的静摩擦因数变小，已足够，木块将仍在原处；如果不变而变小，那么变大，所需的静摩擦因数变大，不够大，木块将下滑，以便因的减小而使所需的减小，才能在新的位置上保持平衡.
和、的粗略图像如图丁所示.
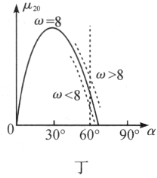
用同样的方法可看出：如果木块向上滑动，它将停留在该处；如果木块向下滑动，它将返回；若增加，木块将向上移动；若减小，木块将停留在该处.
本题的前两问是非惯性系中的静平衡问题，难度不大，但摩擦力的方向因不同的值而变化，这一变化隐含在表达式与具体的数据中，能否挖掘出来，值得阅读时思考.
对于问题（3），首先是答题者能否正确木块的稳定取决于
与、之间的制约. 其次则是否从与、的关系式中分析出在微扰情况下的稳定性. 显然，用解析方式进行分析，难度是可以预料的，能否顺利地转化为用图像进行讨论，成为能否解答的关键. 再次，则是答题者能否顺利地完成作图，并依据图像作出定性分析，这是答题者能否正确解答的最后障碍了.
其实，每一块知识都有一些“超难”的试题，这些试题即便你能顺利阅读，甚至短时间内也能在练习中复现，但并不等于你已经完全掌握，因为，不久以后，你仍然不能独立地完成对它的解答. 但这并不是我们不阅读、不训练这类试题的理由，因为，这类试题的解答一定会给我们示范一些复杂问题的处理方式，而这些处理方式往往会被我们迁移至其他的一些并不难的习题解答之中，这正是我们学习与训练此类习题的初衷.
