题目内容
【题目】设不等式﹣2＜|x﹣1|﹣|x+2|＜0的解集为M，a，b∈M．
（1）证明：| 
|＜ 
；
（2）比较|1﹣4ab|与2|a﹣b|的大小，并说明理由．
【答案】证明：（1）记f （x）=|x﹣1|﹣|x+2|，
则f（x）=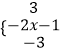 
， 
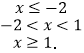，所以解得﹣ 
＜x＜ ，故M=（﹣ ， ）．
所以，| 
|≤ 
|a|+ 
|b|＜ × + × = 
．
解：（2）由（1）得0≤a2＜ ，0≤b2＜ ．
|1﹣4ab|2﹣4|a﹣b|2=（1﹣8ab+16a2b2）﹣4（a2﹣2ab+b2）=4（a2﹣1）（b2﹣1）＞0．
所以，|1﹣4ab|＞2|a﹣b|．
【解析】（1）先去掉函数f（x）的绝对值，得到集合M，再利用基本不等式即可证明；（2）将两个含绝对值的式子平方后进行比较，其平方后的大小关系与平方前一致.
练习册系列答案
相关题目
