Question

【题目】已知函数f（x）=|x﹣5|﹣|x﹣2|．
（1）若x∈R，使得f（x）≤m成立，求m的范围；
（2）求不等式x2﹣8x+15+f（x）≤0的解集．

Answer 1

【答案】
（1）解： ，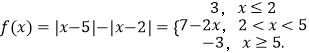
当2＜x＜5时，﹣3＜7﹣2x＜3，

所以﹣3≤f（x）≤3，

∴m≥﹣3；

（2）不等式x2﹣8x+15+f（x）≤0，

即﹣f（x）≥x2﹣8x+15由（1）可知，

当x≤2时，﹣f（x）≥x2﹣8x+15的解集为空集；

当2＜x＜5时，﹣f（x）≥x2﹣8x+15，

即x2﹣10x+22≤0，∴ ；

当x≥5时，﹣f（x）≥x2﹣8x+15，

即x2﹣8x+12≤0，∴5≤x≤6；

综上，原不等式的解集为 ．

【解析】（1）分零点区间讨论，得到分段函数，进而得到f（x）的值域，x∈R，使得f（x）≤m成立，只需m≥﹣3即可，（2）结合（1）中，进行分段讨论，解出不等式即可.