题目内容
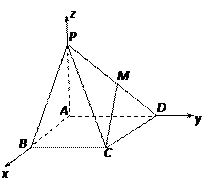
((本小题满分12分)如图,在四棱锥P—ABCD中,
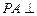 底面ABCD,底面为直角梯形,
底面ABCD,底面为直角梯形,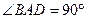 ,
,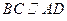 且AD=2,AB=BC=1,PA=
且AD=2,AB=BC=1,PA=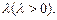
(Ⅰ)设M为PD的中点,求证:
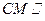 平面PAB;
平面PAB;(Ⅱ)若二面角B—PC—D的大小为150°,求此四棱锥的体积.
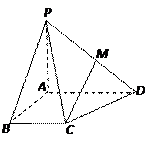
解法一:(Ⅰ)证明:取PA的中点N,连结BN、NM,

在△PAD中,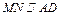 ,且
,且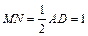 ;
;
又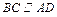 ,且
,且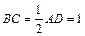 ,
,
所以MN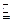 BC,即四边形BCMN为平行四边形,
BC,即四边形BCMN为平行四边形,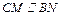 .
.
又 平面PAB,
平面PAB,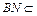 平面PAB,故
平面PAB,故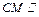 平面PAB. ……5分
平面PAB. ……5分
(Ⅱ)如图,连结AC,则二面角B—PC—D的大小等于二面角B—PC—A的大小与二面角D—PC—A的大小的和. 由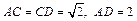 知
知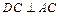 ,又
,又 ,所以
,所以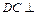 平面PAC,即平面P
平面PAC,即平面P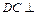 平面PAC,所以二面角D—PC—A的大小为90°. 于是二面角B—PC—A的大小为60°,过B作
平面PAC,所以二面角D—PC—A的大小为90°. 于是二面角B—PC—A的大小为60°,过B作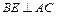 于E,过E作
于E,过E作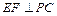 于F,连结BF,由三垂线定理知
于F,连结BF,由三垂线定理知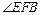 为二面角B—PC—A的平面角. ……9分
为二面角B—PC—A的平面角. ……9分
在Rt△ABC中, ,又易知△PBC为Rt△,且
,又易知△PBC为Rt△,且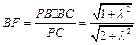 ,
,
∴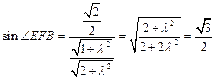 ,解得
,解得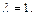 ……11分
……11分
所以四棱锥P—ABCD的体积为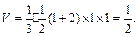 ……12分
……12分
解法二:以A为坐标原点,以AB、AD、AP所在直线为x、y、z轴建立如图所示的空间直角坐标系. 则B(1,0,0),C(1,1,0),D(0,2,0),P(0,0,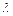 ). ……2分
). ……2分
(Ⅱ)由M为PD中点知M的坐标为(0,1,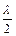 ),所以
),所以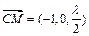 .
.
又平面PAB的法向量可取为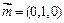 ,而
,而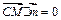 ,即
,即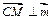 .
.
又 平面PAB,所以
平面PAB,所以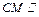 平面PAB. ……6分
平面PAB. ……6分
 (Ⅱ)设平面PBC的法向量为
(Ⅱ)设平面PBC的法向量为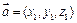 .
.
∵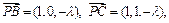 ∴
∴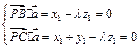
不妨取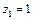 ,则
,则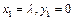 ,∴
,∴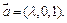
又设平面PCD的法向量为 .
.
∵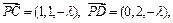 ∴
∴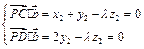
不妨取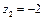 ,则
,则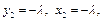 ∴
∴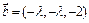 . ……9分
. ……9分
由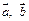 的方向可知
的方向可知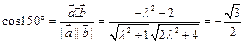 ,解得
,解得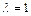 . ……11分
. ……11分
所以四棱锥P—ABCD—体积为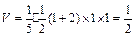 . ……12分解析:
. ……12分解析:
略

在△PAD中,
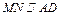 ,且
,且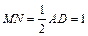 ;
;又
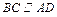 ,且
,且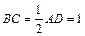 ,
,所以MN
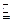 BC,即四边形BCMN为平行四边形,
BC,即四边形BCMN为平行四边形,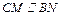 .
.又
 平面PAB,
平面PAB,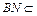 平面PAB,故
平面PAB,故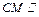 平面PAB. ……5分
平面PAB. ……5分(Ⅱ)如图,连结AC,则二面角B—PC—D的大小等于二面角B—PC—A的大小与二面角D—PC—A的大小的和. 由
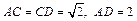 知
知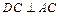 ,又
,又 ,所以
,所以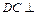 平面PAC,即平面P
平面PAC,即平面P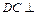 平面PAC,所以二面角D—PC—A的大小为90°. 于是二面角B—PC—A的大小为60°,过B作
平面PAC,所以二面角D—PC—A的大小为90°. 于是二面角B—PC—A的大小为60°,过B作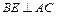 于E,过E作
于E,过E作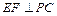 于F,连结BF,由三垂线定理知
于F,连结BF,由三垂线定理知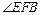 为二面角B—PC—A的平面角. ……9分
为二面角B—PC—A的平面角. ……9分在Rt△ABC中,
 ,又易知△PBC为Rt△,且
,又易知△PBC为Rt△,且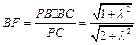 ,
,∴
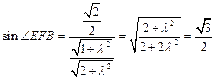 ,解得
,解得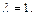 ……11分
……11分所以四棱锥P—ABCD的体积为
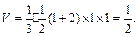 ……12分
……12分 |
解法二:以A为坐标原点,以AB、AD、AP所在直线为x、y、z轴建立如图所示的空间直角坐标系. 则B(1,0,0),C(1,1,0),D(0,2,0),P(0,0,
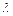 ). ……2分
). ……2分(Ⅱ)由M为PD中点知M的坐标为(0,1,
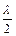 ),所以
),所以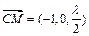 .
.又平面PAB的法向量可取为
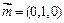 ,而
,而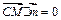 ,即
,即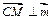 .
.又
 平面PAB,所以
平面PAB,所以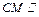 平面PAB. ……6分
平面PAB. ……6分 (Ⅱ)设平面PBC的法向量为
(Ⅱ)设平面PBC的法向量为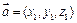 .
. ∵
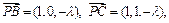 ∴
∴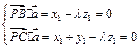
不妨取
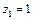 ,则
,则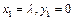 ,∴
,∴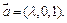
又设平面PCD的法向量为
 .
. ∵
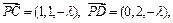 ∴
∴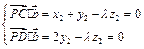
不妨取
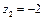 ,则
,则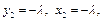 ∴
∴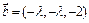 . ……9分
. ……9分由
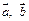 的方向可知
的方向可知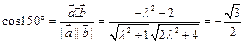 ,解得
,解得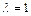 . ……11分
. ……11分所以四棱锥P—ABCD—体积为
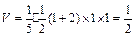 . ……12分解析:
. ……12分解析:略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
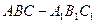 中, AC=4,CB=2,AA1=2
中, AC=4,CB=2,AA1=2
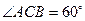 ,E、F分别是
,E、F分别是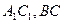 的中点。
的中点。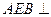 平面
平面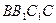 ;
;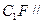 平面ABE;
平面ABE;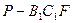 的体积。
的体积。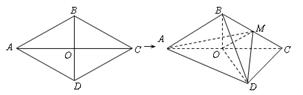
 的边长为
的边长为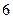 ,
, ,
,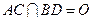 .将菱形
.将菱形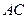 折起,得到三棱锥
折起,得到三棱锥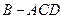 ,点
,点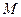 是棱
是棱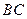 的中点,
的中点,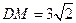 .
.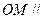 平面
平面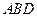 ;
;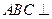 平面
平面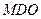 ;
;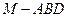 的体积.
的体积.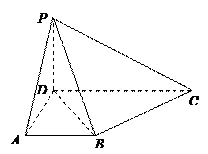
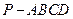 中,侧面
中,侧面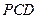
 底面
底面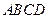 ,
,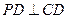 ,底面
,底面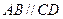 ,
,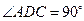 ,
,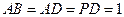 ,
,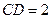 .
.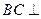 平面
平面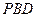 ;
; 为侧棱
为侧棱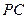 上一点,
上一点,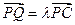 ,
,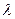 的值,使得二面角
的值,使得二面角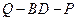 为
为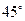 .
.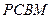 是直角梯形,∠
是直角梯形,∠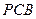 =90°,
=90°,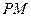 ∥
∥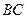 ,
,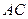 =1,∠
=1,∠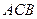 =120°,
=120°,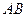 ⊥
⊥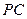 ,直线
,直线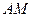 与直线
与直线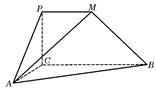
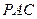 ⊥平面
⊥平面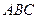 ;
;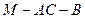 的余弦值.
的余弦值.