题目内容
(本小题满分12分)在直三棱柱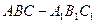 中, AC=4,CB=2,AA1=2
中, AC=4,CB=2,AA1=2
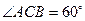 ,E、F分别是
,E、F分别是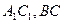 的中点。
的中点。(1)证明:平面
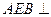 平面
平面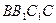 ;
;(2)证明:
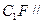 平面ABE;
平面ABE;(3)设P是BE的中点,求三棱锥
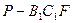 的体积。
的体积。
(1),(2)略;(3)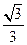 解析:
解析:
 (1)证明:在
(1)证明:在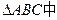 ,∵AC=2BC=4,
,∵AC=2BC=4,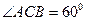
∴ ∴
∴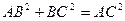
∴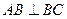 由已知
由已知
∴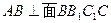
又∵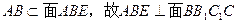 ………………4分
………………4分
(2)证明:取AC的中点M,连结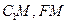
在 ,
,
∴ 直线FM//面ABE
在矩形 中,E、M都是中点
中,E、M都是中点
∴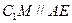 ∴直线
∴直线
又∵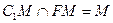 ∴
∴
故 …………………………8分
…………………………8分
(3)在棱AC上取中点G,连结EG、BG,在BG上取中点O,连结PO,则PO// ,
,
 点P到面
点P到面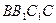 的距离等于点O到平面
的距离等于点O到平面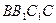 的距离。
的距离。
过O作OH//AB交BC与H,则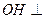 平面
平面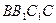
在等边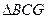 中可知
中可知
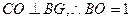 在
在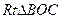 中,可得
中,可得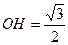
 …………12分
…………12分
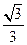 解析:
解析: (1)证明:在
(1)证明:在 ,∵AC=2BC=4,
,∵AC=2BC=4,
∴
 ∴
∴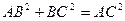
∴
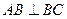 由已知
由已知
∴
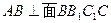
又∵
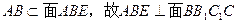 ………………4分
………………4分(2)证明:取AC的中点M,连结
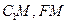
在
 ,
,∴ 直线FM//面ABE
在矩形
 中,E、M都是中点
中,E、M都是中点∴
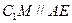 ∴直线
∴直线
又∵
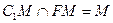 ∴
∴
故
 …………………………8分
…………………………8分(3)在棱AC上取中点G,连结EG、BG,在BG上取中点O,连结PO,则PO//
 ,
, 点P到面
点P到面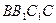 的距离等于点O到平面
的距离等于点O到平面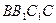 的距离。
的距离。过O作OH//AB交BC与H,则
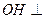 平面
平面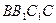
在等边
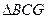 中可知
中可知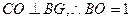 在
在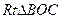 中,可得
中,可得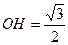
 …………12分
…………12分 
练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
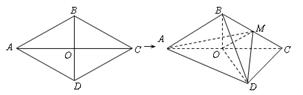
 的边长为
的边长为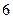 ,
, ,
,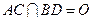 .将菱形
.将菱形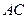 折起,得到三棱锥
折起,得到三棱锥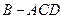 ,点
,点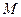 是棱
是棱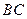 的中点,
的中点,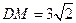 .
.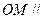 平面
平面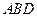 ;
;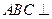 平面
平面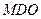 ;
;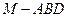 的体积.
的体积.
 中,侧面
中,侧面
 底面
底面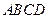 ,
,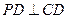 ,底面
,底面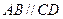 ,
,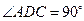 ,
,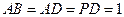 ,
,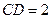 .
.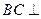 平面
平面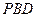 ;
; 为侧棱
为侧棱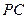 上一点,
上一点,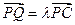 ,
,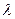 的值,使得二面角
的值,使得二面角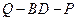 为
为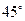 .
.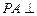 底面ABCD,底面为直角梯形,
底面ABCD,底面为直角梯形,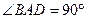 ,
,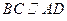 且AD=2,AB=BC=1,PA=
且AD=2,AB=BC=1,PA=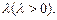
 平面PAB;
平面PAB;
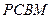 是直角梯形,∠
是直角梯形,∠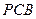 =90°,
=90°,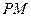 ∥
∥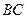 ,
,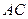 =1,∠
=1,∠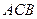 =120°,
=120°,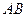 ⊥
⊥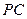 ,直线
,直线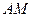 与直线
与直线
 ⊥平面
⊥平面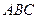 ;
;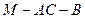 的余弦值.
的余弦值.