题目内容
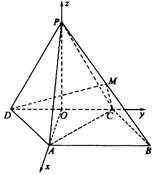
(本小题12分)如图,四棱锥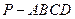 中,
中,侧面
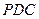 是边长为2的正三角形,且与底面垂直,底面
是边长为2的正三角形,且与底面垂直,底面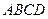 是
是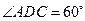 的菱形,
的菱形,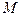 为
为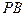 的中点.
的中点.(1)求
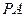 与底面
与底面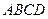 所成角的大小;
所成角的大小;(2)求证:
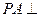 平面
平面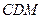 ;
;(3)求二面角
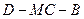 的余弦值.
的余弦值. 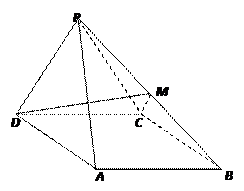
(1)取DC的中点O,由ΔPDC是正三角形,有PO⊥DC.
又∵平面PDC⊥底面ABCD,∴PO⊥平面ABCD于O.
连结OA,则OA是PA在底面上的射影.∴∠PAO就是PA与底面所成角.
∵∠ADC=60°,由已知ΔPCD和ΔACD是全等的正三角形,从而求得OA=OP=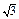 .
.
∴∠PAO=45°.∴PA与底面ABCD可成角的大小为45°.
(2)由底面ABCD为菱形且∠ADC=60°,DC=2,DO=1,有OA⊥DC.
 建立空间直角坐标系如图,则
建立空间直角坐标系如图,则 ,
, 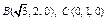 .
.
由M为PB中点,∴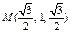 .
.
∴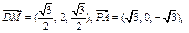
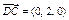 .
.
∴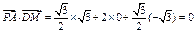 ,
,
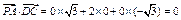 .
.
∴PA⊥DM,PA⊥DC. ∴PA⊥平面DMC.
(3)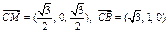 .令平面BMC的法向量
.令平面BMC的法向量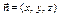 ,
,
则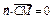 ,从而x+z=0; ……①,
,从而x+z=0; ……①, 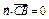 ,从而
,从而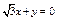 . ……②
. ……②
由①、②,取x=?1,则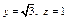 . ∴可取
. ∴可取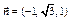 .
.
由(2)知平面CDM的法向量可取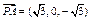 ,
,
∴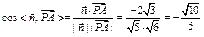 . ∴所求二面角的余弦值为-
. ∴所求二面角的余弦值为-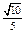 .
.
法二:(1)方法同上
(2)取 的中点
的中点 ,连接
,连接 ,由(Ⅰ)知,在菱形
,由(Ⅰ)知,在菱形 中,由于
中,由于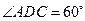 ,则
,则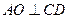 ,又
,又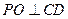 ,则
,则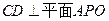 ,即
,即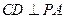 ,
,
又在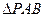 中,中位线
中,中位线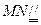
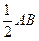 ,
,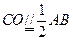 ,则
,则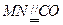 ,则四边形
,则四边形 为
为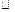 ,所以
,所以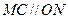 ,在
,在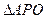 中,
中, ,则
,则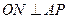 ,故
,故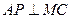 而
而 ,
,
则
(3)由(2)知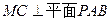 ,则
,则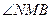 为二面角
为二面角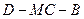 的平面角,在
的平面角,在
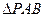 中,易得
中,易得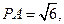
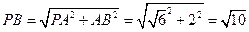 ,
,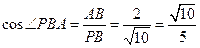 ,
,
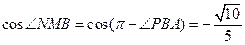 故,所求二面角的余弦值为
故,所求二面角的余弦值为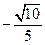 解析:
解析:
略
又∵平面PDC⊥底面ABCD,∴PO⊥平面ABCD于O.
连结OA,则OA是PA在底面上的射影.∴∠PAO就是PA与底面所成角.
∵∠ADC=60°,由已知ΔPCD和ΔACD是全等的正三角形,从而求得OA=OP=
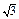 .
.∴∠PAO=45°.∴PA与底面ABCD可成角的大小为45°.
(2)由底面ABCD为菱形且∠ADC=60°,DC=2,DO=1,有OA⊥DC.
 建立空间直角坐标系如图,则
建立空间直角坐标系如图,则 ,
, 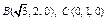 .
.由M为PB中点,∴
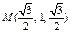 .
.∴
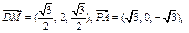
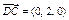 .
.∴
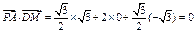 ,
,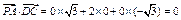 .
.∴PA⊥DM,PA⊥DC. ∴PA⊥平面DMC.
(3)
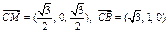 .令平面BMC的法向量
.令平面BMC的法向量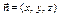 ,
,则
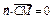 ,从而x+z=0; ……①,
,从而x+z=0; ……①, 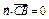 ,从而
,从而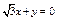 . ……②
. ……②由①、②,取x=?1,则
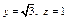 . ∴可取
. ∴可取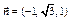 .
.由(2)知平面CDM的法向量可取
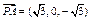 ,
,∴
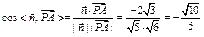 . ∴所求二面角的余弦值为-
. ∴所求二面角的余弦值为-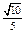 .
.法二:(1)方法同上
(2)取
 的中点
的中点 ,连接
,连接 ,由(Ⅰ)知,在菱形
,由(Ⅰ)知,在菱形 中,由于
中,由于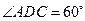 ,则
,则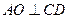 ,又
,又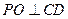 ,则
,则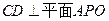 ,即
,即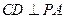 ,
,又在
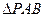 中,中位线
中,中位线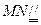
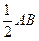 ,
,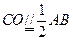 ,则
,则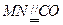 ,则四边形
,则四边形 为
为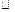 ,所以
,所以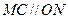 ,在
,在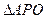 中,
中, ,则
,则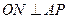 ,故
,故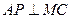 而
而 ,
,则

(3)由(2)知
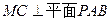 ,则
,则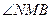 为二面角
为二面角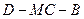 的平面角,在
的平面角,在
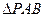 中,易得
中,易得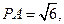
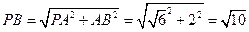 ,
,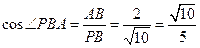 ,
,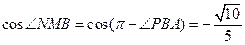 故,所求二面角的余弦值为
故,所求二面角的余弦值为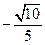 解析:
解析:略

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
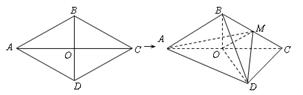
 的边长为
的边长为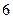 ,
, ,
, .将菱形
.将菱形 折起,得到三棱锥
折起,得到三棱锥 ,点
,点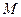 是棱
是棱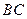 的中点,
的中点,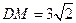 .
.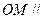 平面
平面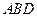 ;
;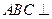 平面
平面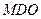 ;
;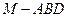 的体积.
的体积.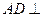 平面
平面 ,
,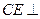 平面
平面 ,
,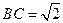 ,
,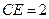 ,
,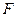 为
为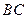 的中点.
的中点.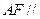 平面
平面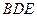 ;
; 平面
平面 .
. 的体积为
的体积为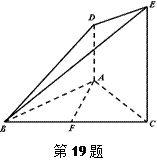
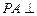 底面ABCD,底面为直角梯形,
底面ABCD,底面为直角梯形,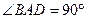 ,
,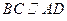 且AD=2,AB=BC=1,PA=
且AD=2,AB=BC=1,PA=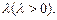
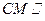 平面PAB;
平面PAB;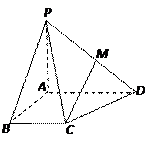
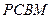 是直角梯形,∠
是直角梯形,∠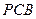 =90°,
=90°,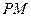 ∥
∥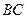 ,
,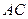 =1,∠
=1,∠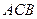 =120°,
=120°,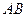 ⊥
⊥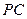 ,直线
,直线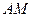 与直线
与直线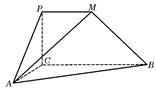
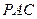 ⊥平面
⊥平面 ;
;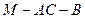 的余弦值.
的余弦值.