题目内容
 如图所示,起重机将一箱设备沿竖直方向匀速吊装到施工高台上,设备重4000N,施工台距离地面的高度为3m.(取g=10N/kg )
如图所示,起重机将一箱设备沿竖直方向匀速吊装到施工高台上,设备重4000N,施工台距离地面的高度为3m.(取g=10N/kg )
(1)起重机的质量为8t,工作时,用支架将汽车的轮胎支离开地面.如果地面能承受的最大压强是7×104Pa,支架与地面接触的总面积是多少?
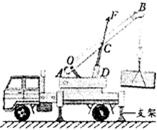
(2)起重臂OA长12m,且与水平方向夹角为30°.支撑臂与起重臂垂直,作用点为B,且OB=4m,求支撑臂给起重臂的支持力(忽略起重臂自重,cos30°≈0.87).
(3)如果动滑轮上每段钢绳的拉力是2500N,求起重机做的额外功和机械效率.
已知:m1=8t=8×103kg,G2=4000N,p=7×104Pa,F=2500N,OA=12m,cos30°≈0.87,h=3m,g=10N/kg
求:(1)支架与地面接触的总面积S;
(2)支撑臂给起重臂的支持力FB;
(3)起重机做的额外功W额和机械效率η.
解:(1)起重机的重力:
G1=m1g=8×103kg×10N/kg=8×104N,
设备重:
G2=4000N,
起重机对地的压力:
F=G1+G2=8×104N+4000N=8.4×104N,
根据压强公式p=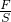 可得,支架的与地的最小接触面积
可得,支架的与地的最小接触面积
S=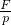 =
= =1.2m2;
=1.2m2;
(2)作用在A点的力:
FA=G2=4000N
由图可知力FA的力臂:
lA=OAcon30°=12m×0.87=10.44m,
根据杠杆平衡条件可得:
FB= =
= =10440N;
=10440N;
(3)绳子自由端移动的距离:
s=2h=2×3m=6m,
拉力做的有用功:
W有=Gh=4000N×3m=1.2×104J,
拉力做的总功:
W总=Fs=2500N×6m=1.5×104J,
额外功:
W额=W总-W有=1.5×104J-1.2×104J=3000J,
起重机的机械效率:
η= ×100%=
×100%= ×100%=80%.
×100%=80%.
答:(1)支架与地面接触的总面积是1.2m2;
(2)支撑臂给起重臂的支持力为10440N;
(3)起重机做的额外功为3000J,机械效率为80%.
分析:(1)支架对地面的压力等于起重机重和设备重之和,又知道地面能承受的最大压强,根据压强公式求出支架与地面接触的总面积;
(2)作用在A点的力和设备的重力相等,利用三角函数可表示出阻力力臂的长,再利用杠杆的平衡条件可求出支撑臂给起重臂支持力的大小;
(3)根据s=nh求出绳子自由端移动的距离,利用W=Gh求出有用功,利用W=Fs求出总功,总功减去有用功即为额外功,然后利用效率公式求出起重机的机械效率.
点评:本题中综合考查了多个力学公式的运用,包括功、功率、机械效率、压强、杠杆的平衡条件等,同时还有对滑轮的分析、杠杆的分析、三角函数的应用等,综合性较强,值得我们认真思考.
求:(1)支架与地面接触的总面积S;
(2)支撑臂给起重臂的支持力FB;
(3)起重机做的额外功W额和机械效率η.
解:(1)起重机的重力:
G1=m1g=8×103kg×10N/kg=8×104N,
设备重:
G2=4000N,
起重机对地的压力:
F=G1+G2=8×104N+4000N=8.4×104N,
根据压强公式p=
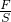 可得,支架的与地的最小接触面积
可得,支架的与地的最小接触面积S=
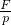 =
= =1.2m2;
=1.2m2;(2)作用在A点的力:
FA=G2=4000N
由图可知力FA的力臂:
lA=OAcon30°=12m×0.87=10.44m,
根据杠杆平衡条件可得:
FB=
 =
= =10440N;
=10440N;(3)绳子自由端移动的距离:
s=2h=2×3m=6m,
拉力做的有用功:
W有=Gh=4000N×3m=1.2×104J,
拉力做的总功:
W总=Fs=2500N×6m=1.5×104J,
额外功:
W额=W总-W有=1.5×104J-1.2×104J=3000J,
起重机的机械效率:
η=
 ×100%=
×100%= ×100%=80%.
×100%=80%.答:(1)支架与地面接触的总面积是1.2m2;
(2)支撑臂给起重臂的支持力为10440N;
(3)起重机做的额外功为3000J,机械效率为80%.
分析:(1)支架对地面的压力等于起重机重和设备重之和,又知道地面能承受的最大压强,根据压强公式求出支架与地面接触的总面积;
(2)作用在A点的力和设备的重力相等,利用三角函数可表示出阻力力臂的长,再利用杠杆的平衡条件可求出支撑臂给起重臂支持力的大小;
(3)根据s=nh求出绳子自由端移动的距离,利用W=Gh求出有用功,利用W=Fs求出总功,总功减去有用功即为额外功,然后利用效率公式求出起重机的机械效率.
点评:本题中综合考查了多个力学公式的运用,包括功、功率、机械效率、压强、杠杆的平衡条件等,同时还有对滑轮的分析、杠杆的分析、三角函数的应用等,综合性较强,值得我们认真思考.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在抗震救灾中,为了从垮塌的建筑中尽快地实施救援,营救生命,使用到了大量的汽车起重机.正在家中复习的小陈同学看到救灾现场的救援画面后,在感动之余,找来了一台玩具汽车起重机,进行了探究.
在抗震救灾中,为了从垮塌的建筑中尽快地实施救援,营救生命,使用到了大量的汽车起重机.正在家中复习的小陈同学看到救灾现场的救援画面后,在感动之余,找来了一台玩具汽车起重机,进行了探究. (2011?乐山模拟)如图所示,起重机正将一箱箱设备吊到2m高的施工台上,起重臂下的钢绳是绕在一个动滑轮上的.若每箱设备重4000N,如果起重机沿竖直方向匀速提升一箱设备时,动滑轮上每段钢绳的拉力为2500N,忽略钢绳重和摩擦,求:
(2011?乐山模拟)如图所示,起重机正将一箱箱设备吊到2m高的施工台上,起重臂下的钢绳是绕在一个动滑轮上的.若每箱设备重4000N,如果起重机沿竖直方向匀速提升一箱设备时,动滑轮上每段钢绳的拉力为2500N,忽略钢绳重和摩擦,求: (2013?邢台模拟)如图所示,起重机将一箱设备沿竖直方向匀速吊装到施工高台上,设备重4000N,施工台距离地面的高度为3m.(取g=10N/kg )
(2013?邢台模拟)如图所示,起重机将一箱设备沿竖直方向匀速吊装到施工高台上,设备重4000N,施工台距离地面的高度为3m.(取g=10N/kg ) 如图所示,起重机正将一箱箱设备吊到2m高的施工台上,起重臂下的钢绳是绕在一个动滑轮上的.若每箱设备重4000N,如果起重机沿竖直方向匀速提升一箱设备时,动滑轮上每段钢绳的拉力为2500N,忽略钢绳重和摩擦,求:
如图所示,起重机正将一箱箱设备吊到2m高的施工台上,起重臂下的钢绳是绕在一个动滑轮上的.若每箱设备重4000N,如果起重机沿竖直方向匀速提升一箱设备时,动滑轮上每段钢绳的拉力为2500N,忽略钢绳重和摩擦,求: