题目内容
 (2011?乐山模拟)如图所示,起重机正将一箱箱设备吊到2m高的施工台上,起重臂下的钢绳是绕在一个动滑轮上的.若每箱设备重4000N,如果起重机沿竖直方向匀速提升一箱设备时,动滑轮上每段钢绳的拉力为2500N,忽略钢绳重和摩擦,求:
(2011?乐山模拟)如图所示,起重机正将一箱箱设备吊到2m高的施工台上,起重臂下的钢绳是绕在一个动滑轮上的.若每箱设备重4000N,如果起重机沿竖直方向匀速提升一箱设备时,动滑轮上每段钢绳的拉力为2500N,忽略钢绳重和摩擦,求:(1)起重机提升一箱设备时,对箱子做的有用功是多少?
(2)动滑轮在提升这箱设备时的机械效率是多大?
(3)动滑轮在一次提升两箱设备时的机械效率是多大?
分析:(1)已知箱子的重力和上升的高度,根据公式W=Gh可求对箱子做的有用功;
(2)已知动滑轮上绳子的拉力和动滑轮上绳子的段数,以及物体升高的高度,根据公式W=Fs可求起重机所做的总功;有用功与总功的比值就是动滑轮的机械效率.
(3)根据F=
(G+G动)求出动滑轮重,根据η=
=
=
求出机械效率.
(2)已知动滑轮上绳子的拉力和动滑轮上绳子的段数,以及物体升高的高度,根据公式W=Fs可求起重机所做的总功;有用功与总功的比值就是动滑轮的机械效率.
(3)根据F=
| 1 |
| 2 |
| W有用 |
| W总 |
| Gh |
| Gh+G动h |
| G |
| G+G动 |
解答:已知:高度h=2m,设备重G1=4000N,第二次设备重G2=8000N,第一次拉力F1=2500N,n=2
求:(1)对箱子做的有用功W有用=?;(2)机械效率η1=?;(3)提升两箱设备时的机械效率η2=?
解:(1)对箱子做的有用功:
W有用=G1h=4000N×2m=8000J;
(2)拉力移动距离:
s=2h=2×2m=4m,
拉力做的总功:
W总=F1s=2500N×4m=10000J,
机械效率:
η1=
×100%=
×100%=80%;
(3)∵F=
(G+G动)
∴动滑轮重G动=2F1-G1=2×2500N-4000N=1000N,
η=
×100%=
×100%=
×100%=
×100%≈88.9%.
答:(1)对箱子做的有用功是8000J;
(2)提升这箱设备时的机械效率是80%;
(3)提升两箱设备时的机械效率88.9%.
求:(1)对箱子做的有用功W有用=?;(2)机械效率η1=?;(3)提升两箱设备时的机械效率η2=?
解:(1)对箱子做的有用功:
W有用=G1h=4000N×2m=8000J;
(2)拉力移动距离:
s=2h=2×2m=4m,
拉力做的总功:
W总=F1s=2500N×4m=10000J,
机械效率:
η1=
| W有用 |
| W总 |
| 8000J |
| 10000J |
(3)∵F=
| 1 |
| 2 |
∴动滑轮重G动=2F1-G1=2×2500N-4000N=1000N,
η=
| W有用 |
| W总 |
| Gh |
| Gh+G动h |
| G2 |
| G2+G动 |
| 8000N |
| 8000N+1000N |
答:(1)对箱子做的有用功是8000J;
(2)提升这箱设备时的机械效率是80%;
(3)提升两箱设备时的机械效率88.9%.
点评:本题考查的是有用功、总功和机械效率的计算,关键是公式及其变形的灵活运用,难点是求动滑轮重的计算.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
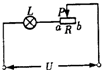 (2011?乐山模拟)如图所示,一个标有“6V,3.6W”字样的小灯泡L和最大阻值为50Ω的滑动变阻器R串联后接在电源电压U恒为6V的电路中,设灯泡电阻不变,则下列判断不正确的是( )
(2011?乐山模拟)如图所示,一个标有“6V,3.6W”字样的小灯泡L和最大阻值为50Ω的滑动变阻器R串联后接在电源电压U恒为6V的电路中,设灯泡电阻不变,则下列判断不正确的是( )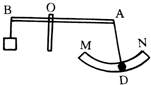 (2011?乐山模拟)如图所示,杠杆AB可绕O转动,绳AD连在以A为圆心的弧形槽MN上,D可以在MN上自由滑动,在绳的D端从N向M滑动过程中杠杆仍保持平衡,则绳对杠杆的拉力变化情况是( )
(2011?乐山模拟)如图所示,杠杆AB可绕O转动,绳AD连在以A为圆心的弧形槽MN上,D可以在MN上自由滑动,在绳的D端从N向M滑动过程中杠杆仍保持平衡,则绳对杠杆的拉力变化情况是( )