��Ŀ����
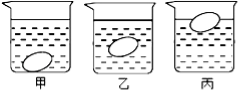
����Ŀ����ͼ��ʾ��������ȫ��ͬ����ϸ���ɣ�ԭ����ΪL0=20cm����ͼ�г�����ľ�鱻�������Ž�û��ˮ�У���ͼ�г�����ʯ�鱻�������Ž�û��ˮ�У�ľ���ʯ�������ͬ��ľ���ʯ�龲ֹʱ�����ɳ��Ⱦ�ΪL=30cm����֪��ľ������Gľ=10N��ˮ��ľ���ܶȹ�ϵ��ˮ=2��ľ �� ��ˮ=1��103kg/m3�����Ե������ܸ�������
�����ͼ��ľ�����ܸ�����
�������ɵĵ���������ɣ�F=k��L��L0������kֵ��������ֵ�͵�λ����
����ʯ����ܶ�. 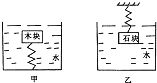
���𰸡��⣺������֪����ˮ=2��ľ
����G=mg�ͦ�= ![]() �ɵã�ľ�������Gľ=��ľVľg
�ɵã�ľ�������Gľ=��ľVľg
ľ����ȫ��û��ˮ�У��ſ�ˮ��������������������
��ľ���ܵ��ĸ�����F��=��ˮgVľ
�ɵã�F��=2Gľ=2��10N=20N��
�ڶԼ�ͼ�е�ľ���������������֪��ľ���������������͵����������¾�ֹ������ƽ��״̬���У�F��+Gľ=F�� ��
��F��=F����Gľ=20N��10N=10N��
F��=k��L��L0���ɵã�10N=k��30cm��20cm����
��ã�k=1N/cm��
�۶���ͼ�е�ʯ���������������֪��ʯ���������������͵����������¾�ֹ������ƽ��״̬���У�F��+ ![]() =Gʯ ��
=Gʯ ��
��Ϊľ���ʯ�������ͬ������û��ˮ�У��ſ�ˮ�������ȣ�
���ԣ������ܵ��ĸ�������ľ���ܵ��ĸ������� ![]() =F��=20N��
=F��=20N��
��Gʯ=F��+ ![]() =10N+20N=30N��
=10N+20N=30N��
��ΪGʯ=��ʯVʯg![]() =��ˮgVʯ �� ��Vʯ=
=��ˮgVʯ �� ��Vʯ= ![]()
��ʯ=1.5��ˮ=1.5��1��103kg/m3=1.5��103kg/m3 ��
�𣺢ټ�ͼ��ľ�����ܸ���Ϊ20N���������ɵĵ���������ɣ�F=k��L��L0����kֵΪ1N/cm����ʯ����ܶ�Ϊ1.5��103kg/m3 ��
���������ٸ���G=mg�ͦ�= ![]() �г�ľ�����������ʽ�����ݰ�����ԭ���г�ľ���ܵ��ĸ����ı���ʽ����֪��ˮ=2��ľ �� ������ʽ����ͼ��ľ�����ܸ������ڶԼ�ͼ�е�ľ�����������������������ƽ����õ�����С��Ȼ�����F=k��L��L0������k��ֵ���۶���ͼ�е�ʯ�����������������������ƽ�����ʯ�������Ĵ�С��Ȼ�����G=mg�ͦ�=
�г�ľ�����������ʽ�����ݰ�����ԭ���г�ľ���ܵ��ĸ����ı���ʽ����֪��ˮ=2��ľ �� ������ʽ����ͼ��ľ�����ܸ������ڶԼ�ͼ�е�ľ�����������������������ƽ����õ�����С��Ȼ�����F=k��L��L0������k��ֵ���۶���ͼ�е�ʯ�����������������������ƽ�����ʯ�������Ĵ�С��Ȼ�����G=mg�ͦ�= ![]() �г�ʯ�����������ʽ�����ݰ�����ԭ���г�ʯ���ܵ��ĸ����ı���ʽ���������ʯ����ܶȣ�
�г�ʯ�����������ʽ�����ݰ�����ԭ���г�ʯ���ܵ��ĸ����ı���ʽ���������ʯ����ܶȣ�
���⿼�鸡�����ܶȵļ��㣬�漰���������ܶȹ�ʽ��Ӧ�ã�������ԭ������������������������Լ����ĺϳ���Ӧ�ã���һ����ѧ�ۺ��⣬�ؼ��ж���һ�Ǹ��ֹ�ʽ������ε�������ã����Ǹ��ݰ�����ԭ���ó�ľ���ʯ�����ܸ�����ȣ��ѶȽϴ�
�����㾫�������ڱ��⿼����ܶȵļ�������ĺϳ���Ӧ�ã���Ҫ�˽��ܶȹ�ʽ���� = m/v�������֪�������Ĵ�С�ͷ���������Ĵ�С�ͷ����Ϊ���ĺϳɣ��������ʱ��һ��Ҫע�����ķ��� ע�⣺ͬһֱ���ϵ���������������ͬʱ�������ش������е��κ�һ�����������෴������������С���ʱ������Ϊ0����С����ʱ������һ��С�ڽϴ���������ܴ��ڽ�С������Ҳ����С�ڽ�С�������ܵó���ȷ�𰸣�

 ����ѵ��ϵ�д�
����ѵ��ϵ�д� ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�