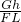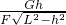题目内容
如图,斜面长为L、高为h,物体重为G,用一个水平推力F将物体匀速推上斜面的顶端.则下列说法正确的是( )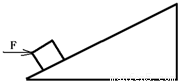
A.斜面的效率为η=

B.斜面的效率为η=

C.斜面对物体的摩擦力为f=(FL-Gh)/L
D.力F对物体所做的功,等于物体机械能的增加值
【答案】分析:(1)斜面是用来提高物体位置的,有用功等于物体重力和斜面高度的乘积,即W有用=Gh;总功等于水平推力和在水平推力方向上移动距离的乘积,即W总=Fs;机械效率就是有用功和总功的比值.
(2)拉力做的功W等于克服物体重力所做的功Gh和克服物体受到的摩擦力所做的功fL之和,从而求出物体所受摩擦力大小.
(3)力对物体做的功为总功,等于物体机械能的增加和克服摩擦做的额外功之和.
解答:解:∵斜面的高为h,物体的重力为G,
∴有用功为:W有用=Gh,
又∵斜面长为L,高为h,所以物体在水平方向上移动的距离为s= ,水平推力为F,
,水平推力为F,
∴总功为:W总=Fs=F ,
,
则机械效率为:η= =
=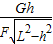 ,故A错误,B正确;
,故A错误,B正确;
∵W总=W有用+W额,
∴克服摩擦做的额外功:
W额=W总-W有用=F -Gh,
-Gh,
∵W额=fL,
∴斜面对物体的摩擦力为f= ,故C错误;
,故C错误;
力对物体做的功为总功,等于物体机械能的增加和克服摩擦做的额外功之和,故D错误.
故选B.
点评:本题考查的是功的计算和有关斜面机械效率的计算,弄清楚在水平力的方向上移动的距离是解决此题的关键关键,知道使用斜面时克服摩擦力做的功就是额外功,关键在于明确总功应等于有用功与额外功之和.
(2)拉力做的功W等于克服物体重力所做的功Gh和克服物体受到的摩擦力所做的功fL之和,从而求出物体所受摩擦力大小.
(3)力对物体做的功为总功,等于物体机械能的增加和克服摩擦做的额外功之和.
解答:解:∵斜面的高为h,物体的重力为G,
∴有用功为:W有用=Gh,
又∵斜面长为L,高为h,所以物体在水平方向上移动的距离为s=
 ,水平推力为F,
,水平推力为F,∴总功为:W总=Fs=F
 ,
,则机械效率为:η=
 =
=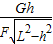 ,故A错误,B正确;
,故A错误,B正确;∵W总=W有用+W额,
∴克服摩擦做的额外功:
W额=W总-W有用=F
 -Gh,
-Gh,∵W额=fL,
∴斜面对物体的摩擦力为f=
 ,故C错误;
,故C错误;力对物体做的功为总功,等于物体机械能的增加和克服摩擦做的额外功之和,故D错误.
故选B.
点评:本题考查的是功的计算和有关斜面机械效率的计算,弄清楚在水平力的方向上移动的距离是解决此题的关键关键,知道使用斜面时克服摩擦力做的功就是额外功,关键在于明确总功应等于有用功与额外功之和.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 一辆小汽车正在匀速爬上黄山一段坡长是1000m、坡高是60m的盘山路,小汽车的质量是1000kg,小汽车的牵引力是720N.
一辆小汽车正在匀速爬上黄山一段坡长是1000m、坡高是60m的盘山路,小汽车的质量是1000kg,小汽车的牵引力是720N.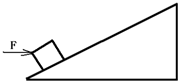 如图,斜面长为L、高为h,物体重为G,用一个水平推力F将物体匀速推上斜面的顶端.则下列说法正确的是( )
如图,斜面长为L、高为h,物体重为G,用一个水平推力F将物体匀速推上斜面的顶端.则下列说法正确的是( ) 利用如图所示的动滑轮将重为G的物体匀速地拉上斜面,设斜面长为L,高为h,滑轮的重力及摩擦力均不计,根据功的原理,则拉力为( )
利用如图所示的动滑轮将重为G的物体匀速地拉上斜面,设斜面长为L,高为h,滑轮的重力及摩擦力均不计,根据功的原理,则拉力为( ) 如图,斜面长为L、高为h,物体重为G,用一个水平推力F将物体匀速推上斜面的顶端.则下列说法正确的是
如图,斜面长为L、高为h,物体重为G,用一个水平推力F将物体匀速推上斜面的顶端.则下列说法正确的是