题目内容
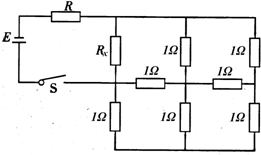 如图所示的电路中,电源电压E=6伏,R=2欧;S为电键;其他8个电阻一个未知,设为Rx.剩下的7个电阻的阻值均为1欧.若闭合电键S以后,电源的输出功率为12瓦,则Rx的阻值为多少?通过Rx中的电流为多少?
如图所示的电路中,电源电压E=6伏,R=2欧;S为电键;其他8个电阻一个未知,设为Rx.剩下的7个电阻的阻值均为1欧.若闭合电键S以后,电源的输出功率为12瓦,则Rx的阻值为多少?通过Rx中的电流为多少?分析:题干中未提及电源内阻,故可以忽略电源的内阻,知道电源的输出功率和电源的电动势,根据P=
求出外电阻的阻值,根据串联电路的电阻特点求出AB之间的总电阻;把AB端口的那包含7个阻值均为1欧的电阻从电路中分离出来,经过两次星三角变换后可得总电阻R0,此时Rx与R0并联,根据电阻的并联特点求出Rx的阻值,根据串联电路的分压特点求出AB部分的电压,利用并联电路的电压特点和欧姆定律求出通过Rx中的电流.
| U2 |
| R |
解答: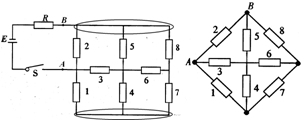 解:由E的6V,输出功率为12W,由P=
解:由E的6V,输出功率为12W,由P=
可得,外电阻的阻值为:
R总=
=
=3Ω,
∵串联电路中总电阻等于各分电阻之和,
∴RAB=R总-R=3Ω-2Ω=1Ω;
如图所示,用圈圈出来的区域电压相同,可以收缩成点,等效电路图如右图所示:
把AB端口的那包含7个阻值均为1欧的电阻从电路中分离出来,
经过两次星三角变换后可得总电阻R0=
Ω,
此时Rx与R0并联,
∵并联电路中总电阻的倒数等于各分电阻倒数之和,
∴
=
+
,
解答:Rx=8Ω,
∵串联电路中各电阻分得的电压与电阻成正比,
∴UAB=
E=
×6V=2V,
∵并联电路中各支路两端的电压相等,
∴根据欧姆定律可得,流过Rx的电流:
Rx=
=
=0.25A.
答:Rx的阻值为8Ω,通过Rx中的电流为0.25A.
 解:由E的6V,输出功率为12W,由P=
解:由E的6V,输出功率为12W,由P=| U2 |
| R |
R总=
| E2 |
| P |
| (6V)2 |
| 12W |
∵串联电路中总电阻等于各分电阻之和,
∴RAB=R总-R=3Ω-2Ω=1Ω;
如图所示,用圈圈出来的区域电压相同,可以收缩成点,等效电路图如右图所示:
把AB端口的那包含7个阻值均为1欧的电阻从电路中分离出来,
经过两次星三角变换后可得总电阻R0=
| 8 |
| 7 |
此时Rx与R0并联,
∵并联电路中总电阻的倒数等于各分电阻倒数之和,
∴
| 1 |
| 1Ω |
| 1 |
| Rx |
| 1 | ||
|
解答:Rx=8Ω,
∵串联电路中各电阻分得的电压与电阻成正比,
∴UAB=
| RAB |
| R总 |
| 1Ω |
| 3Ω |
∵并联电路中各支路两端的电压相等,
∴根据欧姆定律可得,流过Rx的电流:
Rx=
| UAB |
| Rx |
| 2V |
| 8Ω |
答:Rx的阻值为8Ω,通过Rx中的电流为0.25A.
点评:本题考查了串并联电路的特点和欧姆定律、电功率公式的应用,画出AB部分的等效电路图求出7个阻值均为1欧电阻的总电阻是关键.

练习册系列答案
相关题目


 (2013?顺义区一模)在如图所示的电路中,电源两端电压不变.当只闭合开关S1且滑动变阻器R3接入电路电阻值最大时,电压表的示数为3.6V,滑动变阻器消耗的电功率为1.44W,电阻R1消耗的电功率为P1.当只闭合开关S2且滑动变阻器R3的滑片P在中点时,电压表示数为4.5V,电阻R2消耗的电功率为P2.若P1:P2=8:15,则电阻R2在1min40s内所消耗的电能为
(2013?顺义区一模)在如图所示的电路中,电源两端电压不变.当只闭合开关S1且滑动变阻器R3接入电路电阻值最大时,电压表的示数为3.6V,滑动变阻器消耗的电功率为1.44W,电阻R1消耗的电功率为P1.当只闭合开关S2且滑动变阻器R3的滑片P在中点时,电压表示数为4.5V,电阻R2消耗的电功率为P2.若P1:P2=8:15,则电阻R2在1min40s内所消耗的电能为 如图所示的电路中,电源电压为12伏,S断开时,A2表的示数为0.3安;S闭合时,A2表的示数为0.4安,这时A1表的示数为
如图所示的电路中,电源电压为12伏,S断开时,A2表的示数为0.3安;S闭合时,A2表的示数为0.4安,这时A1表的示数为 在如图所示的电路中,电源电压为20伏不变,当S闭合,滑动变阻器的滑片由左向右滑动时,三个电表示数的变化情况是( )
在如图所示的电路中,电源电压为20伏不变,当S闭合,滑动变阻器的滑片由左向右滑动时,三个电表示数的变化情况是( )