题目内容
甲、乙两个实心圆柱体,长度相同,甲的直径为乙的2倍.在两只相同的烧杯中盛有质量相等的水,把甲、乙分别放入其中,水没有溢出.然后把它们分别放在天平左、右托盘中,天平恰能平衡,则甲、乙密度之比ρ甲:ρ乙为
- A.4:1
- B.1:4
- C.2:1
- D.1:2
B
分析:根据甲、乙两圆柱体直径的关系,可以求出甲、乙体积之比;根据天平的平衡情况可以判断二者的质量关系;最后可根据密度的公式,求出它们的密度之比.
解答:根据圆柱体的体积公式,又知道甲、乙的直径之比为2:1,甲、乙两圆柱体的体积之比为:V甲:V乙=S甲h:S乙h=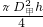 :
: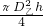 =4:1;
=4:1;
天平平衡,说明两端的总质量相等,又知道烧杯和水的质量分别相等,所以圆柱体的质量相等,即:m甲:m乙=1:1;
将体积之比、质量之比,带入密度的公式得,ρ甲:ρ乙=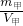 :
: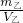 =
= :
: =1:4.
=1:4.
故选B.
点评:利用密度的公式可以进行比值的计算,但此题中还要分清“比值”与“倍数”两种说法之间的转换.
分析:根据甲、乙两圆柱体直径的关系,可以求出甲、乙体积之比;根据天平的平衡情况可以判断二者的质量关系;最后可根据密度的公式,求出它们的密度之比.
解答:根据圆柱体的体积公式,又知道甲、乙的直径之比为2:1,甲、乙两圆柱体的体积之比为:V甲:V乙=S甲h:S乙h=
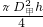 :
: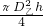 =4:1;
=4:1;天平平衡,说明两端的总质量相等,又知道烧杯和水的质量分别相等,所以圆柱体的质量相等,即:m甲:m乙=1:1;
将体积之比、质量之比,带入密度的公式得,ρ甲:ρ乙=
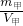 :
: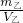 =
= :
: =1:4.
=1:4.故选B.
点评:利用密度的公式可以进行比值的计算,但此题中还要分清“比值”与“倍数”两种说法之间的转换.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,甲、乙两个实心圆柱体放在水平地面上,它们对地面的压强相等,则下列判断正确的是( )
如图所示,甲、乙两个实心圆柱体放在水平地面上,它们对地面的压强相等,则下列判断正确的是( ) 如图所示,甲、乙两个实心圆柱体放在水平地面上,它们对地面的压强相等,则下列判断正确的是( )
如图所示,甲、乙两个实心圆柱体放在水平地面上,它们对地面的压强相等,则下列判断正确的是( )