题目内容
甲、乙两地相距220km,A车用40km/h的速度由甲地向乙地匀速运动,B车用30km/h的速度由乙地向甲地匀速运动.两车同时出发,B车出发后1h,在途中暂停2h后再以原速度继续前进,求两车相遇的时间和地点.
分析:①假设相遇的时间为出发后t小时,即A车行驶了t小时,B车实际行驶了(t-2h),根据题意,相遇时两车运动的距离之和等于220km,由s=vt列式计算;
②综合得出相遇的时间,由s=vt计算出相遇的地点(距离).
②综合得出相遇的时间,由s=vt计算出相遇的地点(距离).
解答:解:①根据题意,相遇时两车运动的距离之和等于220km,设相遇的时间为出发后t小时,根据题意得:
vAt+vB(t-2h)=220km,
即:40km/h×t+30km/h×(t-2h)=220km,
解得t=4h,
故相遇时为出发后4h;
②两车相遇的地点距甲地的距离为:
s甲=vAt=40km/h×4h=160km;
答:两车相遇的时间为出发后4h,相遇的地点距甲地160km.
vAt+vB(t-2h)=220km,
即:40km/h×t+30km/h×(t-2h)=220km,
解得t=4h,
故相遇时为出发后4h;
②两车相遇的地点距甲地的距离为:
s甲=vAt=40km/h×4h=160km;
答:两车相遇的时间为出发后4h,相遇的地点距甲地160km.
点评:本题考查学生对速度公式的应用,关键是搞清楚B车实际行驶了(t-2h),有点难度.

练习册系列答案
相关题目
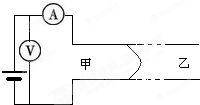 甲、乙两地相距40千米,在甲、乙两地之间沿直线架设两条输电线,已知输电线每千米的电阻为0.2欧.现输电线在某处发生了短路,为确定短路位置,检修员在甲地利用电压表.电流表和电源接成如图所示电路进行测量.当电压表的示数为3.0伏时,电流表的示数为0.5安,则短路位置离甲地的距离为( )
甲、乙两地相距40千米,在甲、乙两地之间沿直线架设两条输电线,已知输电线每千米的电阻为0.2欧.现输电线在某处发生了短路,为确定短路位置,检修员在甲地利用电压表.电流表和电源接成如图所示电路进行测量.当电压表的示数为3.0伏时,电流表的示数为0.5安,则短路位置离甲地的距离为( )| A、10千米 | B、15千米 | C、30千米 | D、40千米 |
某辆汽车以4m/s的速度从甲地开往乙地,当驶完一半时改用6m/s的速度行驶到乙地,甲、乙两地相距2400m,则汽车在甲、乙两地的平均速度为( )
| A、10m/s | B、5m/s | C、4.8m/s | D、6m/s |