题目内容
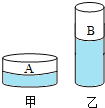
【题目】如图，用甲、乙两个滑轮将同样的钩码缓慢提升相同的高度，（不计绳重和摩擦）则下列说法中正确的是（ ）
A．拉力F1和F2大小相等
B．甲中绳的自由端移动的距离比乙大
C．F1做的总功比F2多
D．甲的机械效率比乙高
【答案】D
【解析】
试题分析：甲是定滑轮绳子的有效股数为1，乙是动滑轮绳子的有效股数为2，根据F=
（G+G动）比较绳端拉力的关系，根据s=nh比较绳端移动距离的关系；不计绳重和摩擦，F1做的总功为克服钩码重力所做的功，F2做的总功为克服钩码和动滑轮重力所做的功，据此可知拉力所做总功的关系；同样的钩码缓慢提升相同的高度时有用功相同，根据η=
×100%可知机械效率的关系．
解：由图知，甲是定滑轮绳子的有效股数为1，乙是动滑轮绳子的有效股数为2；
A．根据定滑轮和动滑轮的特点可得，F1=G，F2=
（G+G动），由于滑轮重和钩码重关系不知，所以拉力F1和F2大小不确定，故A错误；
B．由s=nh可知，s甲=h，s乙=2h，即甲中绳的自由端移动的距离比乙小，故B错误；
C．不计绳重和摩擦，F1做的总功为克服钩码重力所做的功，F2做的总功为克服钩码和动滑轮重力所做的功，则F1做的总功比F2少，故C错误；
D．根据W=Gh可知，用甲、乙两个滑轮将同样的钩码缓慢提升相同的高度时所做的有用功相同，由η=×100%可知，甲拉力做的额外功少，机械效率大，故D正确．
故选D．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
