题目内容
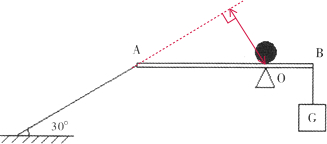
 如图所示,质量不计的光滑木板AB长1.6m,可绕固定点O转动,离O点0.4m的B端挂一重物G,板的A端用一根与水平地面成30°夹角的细绳拉住,木板在水平位置平衡时绳的拉力是8N.然后在O点的正上方放一质量为0.5kg的小球,若小球以20cm/s的速度由O点沿木板向A端匀速运动,问小球至少运动多长时间细绳的拉力减小到零.(取g=10N/kg,绳的重力不计)
如图所示,质量不计的光滑木板AB长1.6m,可绕固定点O转动,离O点0.4m的B端挂一重物G,板的A端用一根与水平地面成30°夹角的细绳拉住,木板在水平位置平衡时绳的拉力是8N.然后在O点的正上方放一质量为0.5kg的小球,若小球以20cm/s的速度由O点沿木板向A端匀速运动,问小球至少运动多长时间细绳的拉力减小到零.(取g=10N/kg,绳的重力不计)分析:掌握杠杆的平衡条件,当球在O点上方时,杠杆在绳的拉力和G的作用下平衡,确定绳的力臂,根据杠杆平衡条件求出G的大小;
当绳的拉力为零时,则杠杆在小球和G的作用下恰好保持平衡,根据杠杆的平衡条件求出小球对杠杆力的力臂,从而根据t=
求出时间.
当绳的拉力为零时,则杠杆在小球和G的作用下恰好保持平衡,根据杠杆的平衡条件求出小球对杠杆力的力臂,从而根据t=
| s |
| v |
解答:解:做出拉力的力臂,如图所示:
根据杠杆平衡条件得:F绳×
AO=G×BO
即:8N×
×(1.6m-0.4m)=G×0.4m
∴G=12N
(2)球的重力G球=m球g=0.5kg×10N/kg=5N
当绳子拉力为0时,设球离O点距离为L球,则根据杠杆平衡条件得:
G球×L球=G×BO
即:5N×L球=12N×0.4m,
∴L球=0.96m=96cm
运动时间t=
=
=4.8s.
答:小球运动4.8s时绳子拉力为零.

根据杠杆平衡条件得:F绳×
| 1 |
| 2 |
即:8N×
| 1 |
| 2 |
∴G=12N
(2)球的重力G球=m球g=0.5kg×10N/kg=5N
当绳子拉力为0时,设球离O点距离为L球,则根据杠杆平衡条件得:
G球×L球=G×BO
即:5N×L球=12N×0.4m,
∴L球=0.96m=96cm
运动时间t=
| L球 |
| v球 |
| 96cm |
| 20cm/s |
答:小球运动4.8s时绳子拉力为零.
点评:此题考查了对杠杆平衡条件的应用,掌握二力平衡条件,并正确地确定杠杆所受的力及对应的力臂,求出物体G的重力是解决此题的关键所在.

练习册系列答案
相关题目
 如图所示,质量不计的光滑木板AB长1.2m,可绕固定点O转动,离O点0.4m的B端挂一重物G,板的A端用一根与水平地面成30°夹角的细绳拉住,木板在水平位置平衡时绳的拉力是9N.求:
如图所示,质量不计的光滑木板AB长1.2m,可绕固定点O转动,离O点0.4m的B端挂一重物G,板的A端用一根与水平地面成30°夹角的细绳拉住,木板在水平位置平衡时绳的拉力是9N.求: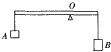 如图所示,质量不计的不等臂杠杆两端分别挂上实心铁球A,B时,恰好能使杠杆在水平位置平衡.若将A和B同时浸没在水中,则杠杆的状态是( )
如图所示,质量不计的不等臂杠杆两端分别挂上实心铁球A,B时,恰好能使杠杆在水平位置平衡.若将A和B同时浸没在水中,则杠杆的状态是( ) 如图所示,质量不计的一块长木板AB可绕O点无摩擦转动,且OA=1m,OB=3m.在A端挂一个配重P,体重为400N的小涛站在B点时,P对地面的压力为300N,当小涛走到距O点
如图所示,质量不计的一块长木板AB可绕O点无摩擦转动,且OA=1m,OB=3m.在A端挂一个配重P,体重为400N的小涛站在B点时,P对地面的压力为300N,当小涛走到距O点