题目内容
如图所示，某人用一根轻质木棒挑一重为120牛的物体放在水平地面上，木棒AB保持水平，棒长AB=1.2米，重物悬挂处离肩膀距离BO=0.8m，则人的肩膀对木棒的支持力为多少牛？若肩膀与B端的距离变小，则肩膀的支持力将怎样变化？分析：选择A为支点，杠杆受肩膀支持力F和重力G的作用，因为木棒保持水平平衡，利用杠杆平衡条件求解．
解答：解：以A为支点，F×LAO=G×LAB
人对棒的支持力：F=G×
=120N×
=360N
由F=G×
当肩与B距离减小时，LAO增大，G、LAB不变
所以肩膀的支持力将变小．
人对棒的支持力：F=G×
| LAB |
| LAO |
| 1.2m |
| 0.4m |
由F=G×
| LAB |
| LAO |
当肩与B距离减小时，LAO增大，G、LAB不变
所以肩膀的支持力将变小．
点评：在杠杆平衡时，可以选择A点为支点是解决本题的关键
练习册系列答案
相关题目
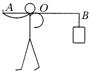21、如图所示，某人用一根轻质木棒挑着重为120N的物体站在水平地面上，木棒保持水平，棒AB长为1.2m，重物悬挂处离肩膀距离BO为0.8m，则手在A端对木棒竖直向下的作用力大小为
如图所示，某人用一根长1m的轻质硬棒去撬动A端一块重500N的石块，已知支点O到A端长20cm，则此杠杆是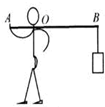
如图所示，某人用一根轻质木棒挑着重为120N的物体站在水平地面上，木棒保持水平，棒AB长为1.2m，重物悬挂处离肩膀距离BO为0.8m，则手在A端对木棒竖直向下的作用力大小为
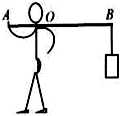如图所示，某人用一根轻质木棒挑着为120N的物体站在水平地面上，木棒保持水平，棒AB长为1.2m，重物悬挂处离肩膀距离BO为0.8m，则手在A端对木棒竖直向下的作用力大小为