Question

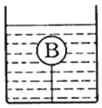
【题目】如图所示，一个半径为r的实心球体处于某种液体中，球体最上端距离液面的距离为h0，已知液体的密度为ρ，球体的体积为πr3．若将此球沿图中虚线切成两个半球，求：

（1）上半球的横切面受到液体向上的压力；

（2）上半球所受的浮力；

（3）液体对球体向下的压力。

Answer 1

【答案】（1）ρg（h0+r）πr2；（2）ρgπr3；（3）ρgπr2（h0+）。

【解析】

（1）将球体分成上、下相等的两个半球，根据液体压强公式求出上半球下底面受到的压强，根据p＝求出下表面受到的压力；

（2）根据阿基米德原理求出上半球受到的浮力；

（3）根据浮力产生的原因（F浮＝F下﹣F上）求出液体对球体向下的压力。

（1）将球体分成上、下相等的两个半球，

上半球下底面大深度为h＝h0+r，

则上半球的横切面受到液体向上的压强：

p＝ρgh＝ρg（h0+r），

由p＝可得，上半球下表面受到的压力：

F下＝pS＝ρg（h0+r）πr2；

（2）上半球受到的浮力：

F浮＝ρgV排1＝ρg×V球＝ρg××πr3＝ρgπr3；

（3）由F浮＝F下﹣F上可得，液体对球体向下的压力：

F上＝F下﹣F浮＝ρg（h0+r）πr2﹣ρgπr3＝ρgh0πr2+ρgπr3＝ρgπr2（h0+）。