题目内容
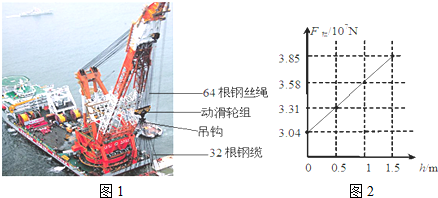
2007年12月22日,在海底23m深处沉睡800多年的“南海一号”古沉船,被“华天龙号”打捞船整体打捞成功.整体打捞是为了保存好文物,将“南海一号”船体和船上满载的货物连带周围的淤泥一起,按照原状固定在特殊的钢制“沉箱”内,沉箱分为上下两部分,上沉箱质量为5000T,底面积为S,高为a=7m,上沉箱整体搬到专门为它建造的广东海上丝绸之路博物馆“水晶宫”内.下沉箱底面积为S,高为5m,打捞过程中将留在海底.“华天龙”打捞船的吊臂臂架长达109m.起吊时,电动机带动绞盘拉动直径为76mm的钢丝绳,钢丝绳总长度2200m,分成64根钢丝绳通过吊臂顶端的定滑轮拉动动滑轮和吊钩,吊钩下用直径为110mm的32根钢缆拴住沉箱的16个吊点,平稳地缓缓竖直上升,上升过程底面始终保持水平,此时钢丝绳的拉力为F1,如图1所示.当沉箱被吊起离开水面,露出高h 时,吊臂对动滑轮组的竖直向上拉力是F拉.它们的数量关系如图2所示.钢丝绳、钢缆所受重力,钢缆在水中的浮力不计,海水的密度为1.0×103kg/m3,g取10N/kg.求:
(1)当沉箱在水底时,海水对上沉箱顶部的压强.
(2)当沉箱在水中匀速竖直上升过程中钢丝绳的拉力F1和机械效率(保留1位小数).
 解:
解:(1)海面至上沉箱的深度为h=23m-12m=11m.
海水对上沉箱顶部的压强:
p=ρ海水gh=1.0×103kg/m3×10N/kg×11m=1.1×105Pa;
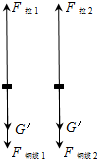
(2)当上沉箱完全浸没在海水时,吊钩和动滑轮组的受力为重力G′,钢缆的拉力F钢缆1,
64根钢丝绳的拉力F拉1,如左图所示,上沉箱匀速上升,F拉1=F钢缆1+G′,
F钢缆1=G沉箱-F浮1
F浮1=ρ海水gV沉箱=ρ海水?g?a?S
F拉1=G沉箱+G′-ρ海水?g?a?S ①
当上沉箱露出海水1m时,吊钩和动滑轮组的受力为重力G′,钢缆的拉力F钢缆2,64根钢丝绳的拉力F拉2,如右图所示,上沉箱匀速上升,F拉2=F钢缆2+G′
F钢缆2=G沉箱-F浮2
F浮2=ρ海水?g?V沉箱′=ρ海水?g?(a-h)?S
F拉2=G沉箱+G′-ρ海水?g?(a-h)?S ②
由题中表格可以知道:F拉1=3.04×107N,F拉2=3.58×107N,
②-①式,得到:F拉2-F拉1=ρ海水?g?a?S-ρ海水?g?(a-h)?S=ρ海水?g?S?h
3.58×107N-3.04×107N=103kg/m3×10N/kg×1m?S
解出:S=5.4×102m2,
G沉箱=m沉箱?g=5×106kg×10N/kg=5×107N,
F浮1=ρ海水?g?V排=5.4×102m2×7m×10N/kg×103kg/m3=3.78×107N,
G′=F拉1-G沉箱+F浮1=3.04×107N-5×107N+3.78×107N=1.82×107N,
钢丝绳的拉力:F1=
 F拉1=
F拉1= ×3.04×107N=4.75×105N;
×3.04×107N=4.75×105N;设沉箱匀速上升lm,则拉力移动距离s=64×1m=64m,
拉力做功W总=F1s=F1×64m,有用功为W有=F钢缆1h=(G-F浮1)×1m,
所以机械效率为:η=
 ×100%=
×100%=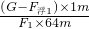 ×100%=
×100%=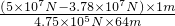 ×100%≈40.1%.
×100%≈40.1%.答:(1)当沉箱在水底时,海水对上沉箱顶部的压强1.1×105Pa;
(2)当沉箱在水中匀速竖直上升过程中钢丝绳的拉力F1为4.75×105N;机械效率为40.1%.
分析:(1)求出上沉箱顶部到水面的深度,根据p=ρgh求出压强;
(2)对沉箱分为两种情况--浸没在水中和离开水面进行受力分析,列出方程组,解出拉力F1的大小;
然后根据公式W=Fs分别求出有用功和总功,根据η=
 求出机械效率.
求出机械效率.点评:此题主要考查的是学生对液体压强、机械效率计算公式和对物体进行受力分析的理解和掌握,根据受力分析列出方程组是解决此题的关键,难度较大.

练习册系列答案
相关题目
 29、2007年12月22日上午,位于海面下几十米深处的“南海一号”商船被打捞浮出海面,这是中国考古史上的又一突破.“南海一号”商船长约30米,是目前发现的最大的宋代船只,如图所示.很早以前,我国考古队员就利用超声波方向性好的特点制成了一种装置安装在船上,用它发出的超声波对“南海一号”沉船进行了细致的探测.
29、2007年12月22日上午,位于海面下几十米深处的“南海一号”商船被打捞浮出海面,这是中国考古史上的又一突破.“南海一号”商船长约30米,是目前发现的最大的宋代船只,如图所示.很早以前,我国考古队员就利用超声波方向性好的特点制成了一种装置安装在船上,用它发出的超声波对“南海一号”沉船进行了细致的探测.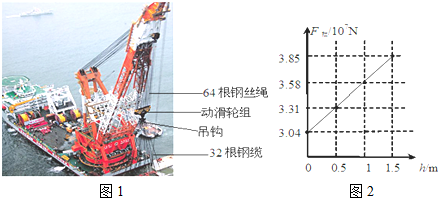
 (2008?黄浦区一模)如图是2007年12月22日“南海一号”整体打捞出海面的情景.在打捞过程中,潜水员要潜入海下将多个未充气的气囊分别均匀地安装在沉箱的四周.潜水员在海面下25米深处受到海水的压强为
(2008?黄浦区一模)如图是2007年12月22日“南海一号”整体打捞出海面的情景.在打捞过程中,潜水员要潜入海下将多个未充气的气囊分别均匀地安装在沉箱的四周.潜水员在海面下25米深处受到海水的压强为